Question

A tube filled with water and closed at both ends uniformly rotates in a horizontal plane about the OO' axis. The manometers A and B fixed in the tube at distances ${r_1}$ ​ and ${r_2}$ from rotational axis indicate pressure ${p_1}$​ and ${p_2}$ ​, respectively. Determine the angular velocity $\omega $ of rotation of the tube:

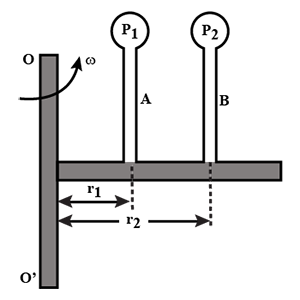
(A) $\omega = \sqrt {\dfrac{{2({p_2} - {p_1})}}{{\rho (r_1^2 - r_2^2)}}} $
(B) $\omega = \sqrt {\dfrac{{2({p_2} - {p_1})}}{{\rho (r_1^2 + r_2^2)}}} $
(C) $\omega = \sqrt {\dfrac{{2(r_2^2 - r_1^2)}}{{({p_2} - {p_1})}}} $
(D) $\omega = \sqrt {\dfrac{{2({p_2} - {p_1})}}{{\rho {r_1}{r_2}}}} $

Answer 1

Hint We know Bernoulli equation relates the speed of the fluid at a point, the pressure at that point and the height of that point above the reference level. Bernoulli equation is given by:
$P + \rho gh + \dfrac{1}{2}\rho {v^2} = $ constant
Since height is the same for both A and B hence $\rho gh$ term can be neglected.

Complete Step by step solution
On applying Bernoulli equation separately for A and B we get,
For A, ${p_1}$ is the reading shown in the barometer.
Hence, \[{p_1} + \rho gh + \dfrac{1}{2}\rho {v_1}^2 = \] constant…… (1)
For B, ${p_2}$ is the reading shown in the barometer.
Hence, \[{p_2} + \rho gh + \dfrac{1}{2}\rho v_2^2 = \] constant…… (2)
From equation (1) and (2) we get
\[
  {p_1} + \rho gh + \dfrac{1}{2}\rho v_1^2 = {p_2} + \rho gh + \dfrac{1}{2}\rho v_2^2 \\
  {p_1} + \dfrac{1}{2}\rho v_1^2 = {p_2} + \dfrac{1}{2}\rho v_2^2 \\
 \]
Now we know that $v = r\omega $
Therefore, above equation becomes
\[
  {p_1}\rho {({r_1}\omega )^2} = {p_2} + \dfrac{1}{2}\rho {({r_2}\omega )^2} \\
  ({p_2} - {p_1}) = \dfrac{1}{2}\rho ({r_1}^2 - {r_2}^2){\omega ^2} \\
  \therefore {\omega ^2} = \dfrac{{2({p_2} - {p_1})}}{{\rho ({r_1}^2 - {r_2}^2)}} \\
    \\
 \]
$\omega = \sqrt {\dfrac{{2({p_2} - {p_1})}}{{\rho (r_1^2 - r_2^2)}}} $
Hence the required angular velocity is, $\omega = \sqrt {\dfrac{{2({p_2} - {p_1})}}{{\rho (r_1^2 - r_2^2)}}} $

Option (A) is correct.

Note Bernoulli equation is just the application of work-energy theorem in the case of fluid flow. In the Bernoulli equation we make a few assumptions like the fluid is ideal i.e. incompressible and nonviscous, it has constant density, both points lie on a streamline, flow is steady and there is no friction.