
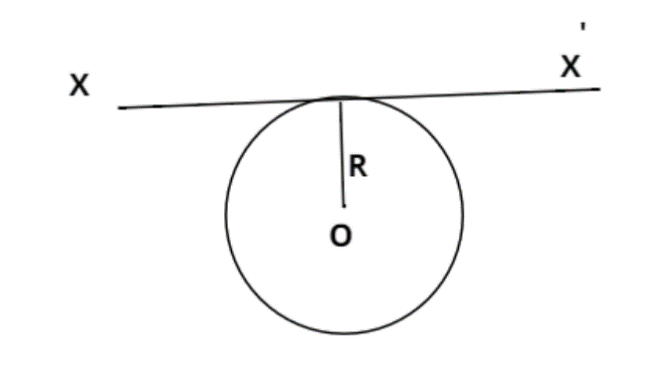
A thin metal wire of length ‘L’ and uniform linear mass density ‘$\rho $’ is bent into a circular coil with ‘o’ as center. The moment of inertia of a coil about the axis $XX'$ is?
$
(a){\text{ }}\dfrac{{3\rho {L^3}}}{{8{\pi ^2}}} \\
(b){\text{ }}\dfrac{{\rho {L^3}}}{{4{\pi ^2}}} \\
(c){\text{ }}\dfrac{{3\rho {L^3}}}{{4{\pi ^2}}} \\
(d){\text{ }}\dfrac{{\rho {L^3}}}{{8{\pi ^2}}} \\
$
Answer
233.1k+ views
Hint: In this question use the concept that the length of the wire will be equal to circumference of the circular coil that is L =$2\pi r$, where r is the radius of the circular coil. The moment of inertia of any circular loop around the tangent is given as $\dfrac{3}{2}m{r^2}$, so use the concept that the mass of the circular coil will be equal to the mass of the thin wire that is$\rho L$. This will help approaching the problem.
Complete step-by-step solution -
Length of thin metal wire = L
And uniform mass density = $\rho $
As we know that the mass of any object is the product of uniform mass density and the length of the object.
Therefore, mass (m) of the thin metal wire = $\rho L$
Now this wire is bent into a circular coil.
So the length of the wire = circumference of the circular coil.
Therefore, L = $2\pi r$, where r is the radius of the circular coil.
$ \Rightarrow r = \dfrac{L}{{2\pi }}$............... (1)
As we know the moment of inertia of the circular coil about the tangent XX’ is given as, $\dfrac{3}{2}m{r^2}$.
Where, m = mass of the circular coil which is equal to the mass of the thin wire = $\rho L$........... (2)
And r = radius of the circular coil.
Let the moment of inertia be denoted by $I$.
So the moment of inertia of a circular coil about the axis XX’ is
$I = \dfrac{3}{2}m{r^2}$
Now substitute the values of (r) and (m) from equation (1) and (2) we have,
$ \Rightarrow I = \dfrac{3}{2}\left( {\rho L} \right){\left( {\dfrac{L}{{2\pi }}} \right)^2}$
Now simplify this we have,
$ \Rightarrow I = \dfrac{3}{2}\left( {\rho L} \right)\left( {\dfrac{{{L^2}}}{{4{\pi ^2}}}} \right) = \dfrac{3}{8}\dfrac{{\rho {L^3}}}{{{\pi ^2}}}$
So this is the required moment of inertia of a circular coil about the axis XX’.
So this is the required answer.
Hence option (A) is the correct answer.
Note – A body has the tendency to resist angular acceleration, so moment of inertia is the measure of tendency of the body to resist this angular acceleration. In general moment of inertia is given as $I = \sum {{m_i}{r_i}^2} $that is it is equal to the sum of the product of each element’s mass and the square of the distance of these elements from the axis about which moment of inertia has to be taken out.
Complete step-by-step solution -
Length of thin metal wire = L
And uniform mass density = $\rho $
As we know that the mass of any object is the product of uniform mass density and the length of the object.
Therefore, mass (m) of the thin metal wire = $\rho L$
Now this wire is bent into a circular coil.
So the length of the wire = circumference of the circular coil.
Therefore, L = $2\pi r$, where r is the radius of the circular coil.
$ \Rightarrow r = \dfrac{L}{{2\pi }}$............... (1)
As we know the moment of inertia of the circular coil about the tangent XX’ is given as, $\dfrac{3}{2}m{r^2}$.
Where, m = mass of the circular coil which is equal to the mass of the thin wire = $\rho L$........... (2)
And r = radius of the circular coil.
Let the moment of inertia be denoted by $I$.
So the moment of inertia of a circular coil about the axis XX’ is
$I = \dfrac{3}{2}m{r^2}$
Now substitute the values of (r) and (m) from equation (1) and (2) we have,
$ \Rightarrow I = \dfrac{3}{2}\left( {\rho L} \right){\left( {\dfrac{L}{{2\pi }}} \right)^2}$
Now simplify this we have,
$ \Rightarrow I = \dfrac{3}{2}\left( {\rho L} \right)\left( {\dfrac{{{L^2}}}{{4{\pi ^2}}}} \right) = \dfrac{3}{8}\dfrac{{\rho {L^3}}}{{{\pi ^2}}}$
So this is the required moment of inertia of a circular coil about the axis XX’.
So this is the required answer.
Hence option (A) is the correct answer.
Note – A body has the tendency to resist angular acceleration, so moment of inertia is the measure of tendency of the body to resist this angular acceleration. In general moment of inertia is given as $I = \sum {{m_i}{r_i}^2} $that is it is equal to the sum of the product of each element’s mass and the square of the distance of these elements from the axis about which moment of inertia has to be taken out.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




