Question

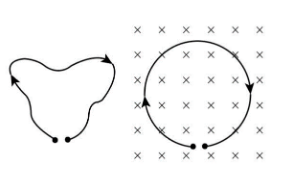
A thin flexible wire of length $L$ is connected to two adjacent fixed points and carries a current $I$ in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is

A. $\left( a \right){\text{ IBL}}$
B. $\left( b \right){\text{ }}\dfrac{{IBL}}{\pi }$
C. $\left( c \right){\text{ }}\dfrac{{IBL}}{{2\pi }}$
D. $\left( d \right){\text{ }}\dfrac{{IBL}}{{4\pi }}$

Answer 1

Hint:The above problem can be solved by using the concept of the magnetic force. The magnetic force is defined as the effect of the current-carrying conductor on the object placed in the magnetic field. The magnetic force on the object depends on the current, magnetic field, length, and direction of the current and magnetic field.

Complete step by step answer:
So we have the values given as
The length of the wire is $L$ .
The current in the wire is $I$ .
The uniform magnetic field around the wire is $B$ .
The expression to calculate the length of the wire is,
$ \Rightarrow L = 2\pi R$
And from here the value of $R$ will be equal to
$ \Rightarrow R = \dfrac{L}{{2\pi }}$
Since the tension in the wire is the same as the magnetic force on the wire.
The expression to calculate the tension in the wire is,
$ \Rightarrow T = BIR$
Now on substituting $\dfrac{L}{{2\pi }}$ for $R$ in the above expression to find the tension in the wire, we get
$ \Rightarrow T = BI\left( {\dfrac{L}{{2\pi }}} \right)$
And on solving it, we get
$ \therefore T = \dfrac{{IBL}}{{2\pi }}$
Thus, the tension in the wire is $\dfrac{{IBL}}{{2\pi }}$ .

Therefore, the option C is the correct answer.

Additional Information:
The variation in the area and magnetic field produces the induced emf in the object. This emf opposes the variation in the magnetic field. The objects placed in the vicinity of the induced emf exert a force on the object.

Note:We can also solve the above question by equating the force acting on the element. So for this, we will consider a small length which will be $dL$ and the radius of the wire will be $R$ .

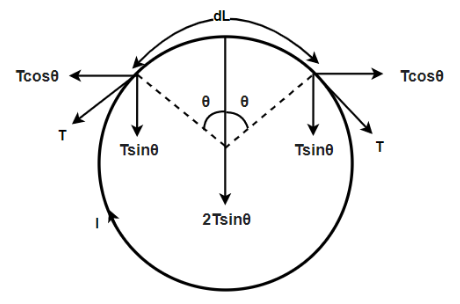
So, the force acting on an element will be equal to,
$ \Rightarrow BI\left( {dL} \right) = 2T\sin \theta $
Since, the value of $\theta $ is very small, therefore
$ \Rightarrow BI\left( {R2\theta } \right) = 2T\theta $
And as we know $L = 2\pi R$
Hence, $T = BIR$
And on putting the value of $T$ , we get the equation as
$ \therefore T = BI\dfrac{L}{{2\pi }}$
Thus, the tension in the wire is $\dfrac{{IBL}}{{2\pi }}$ .
Hence, in this way also we can solve this question.