
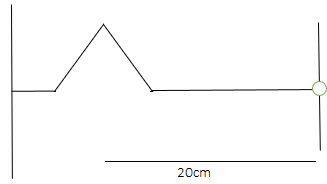
A string of linear mass density \[0.5g\,c{m^{ - 1}}\] and a total length \[30cm\] is tied to a fixed wall at one end and to a frictionless ring at the other end (figure below). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of \[20cm\,{s^{ - 1}}\]. The pulse is symmetric about its maximum which is located at a distance of \[20cm\] from the end joined to the ring.
(a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape.
(b) The shape of the string changes periodically with time. Find this time period.
(c) What is the tension in the string?
Answer
232.8k+ views
Hint: In this question, we see that the wire is traveling from denser to medium so phase change is equal to \[0\]. Now we know that the time is taken by the string formula is \[time = \dfrac{S}{v}\] then we find the tension of the string with the formula \[n = \dfrac{1}{{2l}}\sqrt {\left( {\dfrac{T}{m}} \right)} \,\] . So, by substituting all the given formulas we get the required result.
Formula used:
1. \[\text{Time} = \dfrac{S}{v} \]
Where, s = distance v = wave speed
2. \[n = \dfrac{1}{{2l}}\sqrt {\left( {\dfrac{T}{m}} \right)} \]
where, m = mass per unit length, l = length, T = tension of the string.
Complete step by step solution:
We are given that
mass density \[ = 0.5g\,c{m^{ - 1}}\]
total length\[ = 30cm\]
Speed \[ = 20cm\,{s^{ - 1}}\]
Now we know that the crest reflects as a crest here, as the wire is travelling from denser to rarer medium. Therefore, phase changes are equal to \[0\].
(a) Now to gain the original shape distance travelled by the wave S is
\[S = \left( {20 + 20} \right)cm = 40cm \\ \]
Now wave speed is \[v = 20m/s\]
Therefore,
\[\text{time} = \dfrac{S}{v} = \dfrac{{40}}{{20}} = 20\sec \]
Hence, the time taken is \[20\sec \]
(b) Now the wave regains its shape after travelling a periodic distance is
\[s = 2 \times 30 = 60cm \]
Therefore,
\[\text{time} = \dfrac{s}{v} = \dfrac{{60}}{{20}} = 3\sec \]
Hence, the time period is \[3\sec \]
(c) We know that frequency(n) is inversely proportional to time period
So,
\[n = \dfrac{1}{t} = \dfrac{1}{3}{\sec ^1} \\ \]
We know that
\[n = \dfrac{1}{{2l}}\sqrt {\left( {\dfrac{T}{m}} \right)} \]
By substituting all the values in above, we get
\[\dfrac{1}{3} = \dfrac{1}{{2 \times 30}}\sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \\
\Rightarrow \dfrac{1}{3} = \dfrac{1}{{60}}\sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \\
\Rightarrow \dfrac{{60}}{3} = \sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \\
\Rightarrow 20 = \sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \]
Further solving, we get
\[{\left( {20} \right)^2} = {\left[ {\sqrt {\left( {\dfrac{T}{{0.5}}} \right)} } \right]^2} \\
\Rightarrow 400 = \dfrac{T}{{0.5}} \\
\Rightarrow T = 400 \times 0.5 = 400 \times \dfrac{5}{{10}} \]
Furthermore solving,
\[T = 40 \times 5 \\
\Rightarrow T = 200dyne \\
\Rightarrow T = 2 \times {10^{ - 3}}Newton \]
Hence, tension in the string is \[2 \times {10^{ - 3}}Newton\]
Note: Students must understand all of the formulas used in the solution and be careful when substituting all of the values in the formula; otherwise, calculation errors may occur, and students will not obtain the desired result.
Formula used:
1. \[\text{Time} = \dfrac{S}{v} \]
Where, s = distance v = wave speed
2. \[n = \dfrac{1}{{2l}}\sqrt {\left( {\dfrac{T}{m}} \right)} \]
where, m = mass per unit length, l = length, T = tension of the string.
Complete step by step solution:
We are given that
mass density \[ = 0.5g\,c{m^{ - 1}}\]
total length\[ = 30cm\]
Speed \[ = 20cm\,{s^{ - 1}}\]
Now we know that the crest reflects as a crest here, as the wire is travelling from denser to rarer medium. Therefore, phase changes are equal to \[0\].
(a) Now to gain the original shape distance travelled by the wave S is
\[S = \left( {20 + 20} \right)cm = 40cm \\ \]
Now wave speed is \[v = 20m/s\]
Therefore,
\[\text{time} = \dfrac{S}{v} = \dfrac{{40}}{{20}} = 20\sec \]
Hence, the time taken is \[20\sec \]
(b) Now the wave regains its shape after travelling a periodic distance is
\[s = 2 \times 30 = 60cm \]
Therefore,
\[\text{time} = \dfrac{s}{v} = \dfrac{{60}}{{20}} = 3\sec \]
Hence, the time period is \[3\sec \]
(c) We know that frequency(n) is inversely proportional to time period
So,
\[n = \dfrac{1}{t} = \dfrac{1}{3}{\sec ^1} \\ \]
We know that
\[n = \dfrac{1}{{2l}}\sqrt {\left( {\dfrac{T}{m}} \right)} \]
By substituting all the values in above, we get
\[\dfrac{1}{3} = \dfrac{1}{{2 \times 30}}\sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \\
\Rightarrow \dfrac{1}{3} = \dfrac{1}{{60}}\sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \\
\Rightarrow \dfrac{{60}}{3} = \sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \\
\Rightarrow 20 = \sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \]
Further solving, we get
\[{\left( {20} \right)^2} = {\left[ {\sqrt {\left( {\dfrac{T}{{0.5}}} \right)} } \right]^2} \\
\Rightarrow 400 = \dfrac{T}{{0.5}} \\
\Rightarrow T = 400 \times 0.5 = 400 \times \dfrac{5}{{10}} \]
Furthermore solving,
\[T = 40 \times 5 \\
\Rightarrow T = 200dyne \\
\Rightarrow T = 2 \times {10^{ - 3}}Newton \]
Hence, tension in the string is \[2 \times {10^{ - 3}}Newton\]
Note: Students must understand all of the formulas used in the solution and be careful when substituting all of the values in the formula; otherwise, calculation errors may occur, and students will not obtain the desired result.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




