Question

A straight wire of mass $200\;{\text{g}}$ and length $1.5\;{\text{m}}$ carries a current of $2\;{\text{A}}$. It is suspended in mid-air by a uniform horizontal magnetic field ${\text{B}}$. The magnitude of ${\text{B}}$ (in tesla) is:
(A) \[0.65\]
(B) \[0.55\]
(C) \[0.75\]
(D) \[0.45\]

Answer 1

Hint: As we can all see, the force acting under a uniform magnetic field on a current-carrying wire is equal to the weight of the wire because the wire is in equilibrium and has no acceleration, so it does not move.
Formula Used: We will be using the following formula,
\[F = BiL\sin \theta \]
Where
\[F\] is the force due to the magnetic field
\[B\] is the magnitude of the magnetic field
\[i\] is the current carrying in the wire
\[L\] is the length of the wire
\[\theta \] in the angle between magnetic field and current

Complete Step-by-Step solution:
The following information is provided to us in the given question:
The mass of the wire, \[m = 200g = 0.2kg\]
The length of the wire, \[l = 15m\]
The current flowing through the wire, \[i = 2A\]
And we have to find out the magnetic field
Let us draw the stick figure of the wire given in the question and mention all the forces acting on it

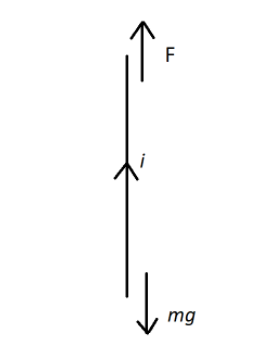
Now, we can see that the direction of current is perpendicular to the magnetic field horizontally, hence the angle
$\theta = {90^\circ }$
We know that
\[F = BiL\sin \theta \]
Since, $\theta = {90^\circ }$, we have \[\sin {90^ \circ } = 1\]
So,
\[F = BiL\]
Now the weight of the wire is given by \[w = mg\]
That is \[w = 0.2 \times 9.8 N\]
According to the figure,
\[F = mg\]
Now, let us substitute the known values in the formula to get
\[BiL = mg\]
Rearranging the terms, we have
\[B = \dfrac{{mg}}{{iL}}\]
Let us now substitute the values
\[B = \dfrac{{0.2 \times 9.8}}{{2 \times 15}}\]
So, we get
\[\therefore B = 0.65 T\]

Hence, the correct option is (A.)

Note: We all learned that the left-hand rule of Fleming is used to describe the force placed at right angles to a magnetic field on a current-carrying conductor. The conductor carrying the current should be made of ferromagnetic material.