Question

A step-up transformer is used to:
A. Increase the current and increase the voltage
B. Decrease the current and increase the voltage
C. Increase the current and decrease the voltage
D. Decrease the current and decrease the voltage

Answer 1

Hint: A Transformer is a static electrical machine which transfers AC electrical power from one circuit to the other circuit at the constant frequency, but the voltage and current through the circuit can be altered that means voltage and the current of the incoming current can be increased or decreased according to the requirement by means of the step-up or step-down transformer.

Complete answer:
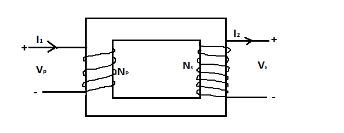
Step-down transformer is used to decrease the voltage while the step-up transformer is used to increase the voltage. Here shown is a step-up transformer since the number of turns in the primary coil is less than the number of turns of the secondary coil, ${N_p} < {N_s}$.

As we all know that the transformation ratio of a transformer is,

The transformation ratio is defined as the ratio of the number of turns in the secondary winding to the number of turns in the primary winding.
$T.R. = \dfrac{{{N_s}}}{{{N_p}}}$
Also, the transformation ratio is the ratio of voltage at the secondary terminal to the voltage at the primary terminals.
So, we get $T.R. = \dfrac{{{N_s}}}{{{N_p}}} = \dfrac{{{V_s}}}{{{V_p}}}$-----equation (1)
Also, we know that power is equal to the voltage multiplied by the current.
$P = VI$, where $P = $power, $V = $voltage and $I = $current.
since the frequency will be the same at input and output that means the power will also be same at the input and the output.
So we can write as $\dfrac{P}{{{I_s}}}$and $\dfrac{P}{{{I_p}}}$ in place of ${V_s}$ and ${V_p}$respectively.
So, from equation we get,
$T.R. = \dfrac{{{N_s}}}{{{N_p}}} = \dfrac{{{V_s}}}{{{V_p}}} = \dfrac{{\dfrac{P}{{{I_s}}}}}{{\dfrac{P}{{{I_p}}}}} = \dfrac{{{I_p}}}{{{I_s}}}$
So, we can write like,
$ \Rightarrow \dfrac{{{V_s}}}{{{V_p}}} = \dfrac{{{I_p}}}{{{I_s}}}$
This shows that when voltage will increase then the current will decrease in a step-up transformer.

So, the correct answer is “Option B”.

Note:
The advantages of the use of step-up transformers-

i)It allows the transmission of the electricity over long distances with minimal loss.
ii)It is quite economical because it requires only installation cost and the maintenance is low.
iii)It works non-stop for a very long period of time.
iv)It requires no starting time.

Step-up transformers are used at power stations to produce the very high voltages which are needed to be transmitted through the National Grid power lines. The high voltages which are getting generated are very dangerous to use in the home, so here the role of the step-down transformers also come into picture, so step-down transformers are used locally to reduce the voltage to safe levels to safely use for households.