
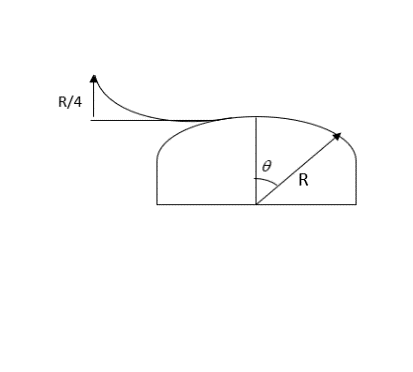
A skier plans to ski a smoothly fixed hemisphere of the radius $R$. He starts from rest from a curved smooth surface of height $\dfrac{R}{4}$. The angle $\theta $ at which he leaves the hemisphere is:
$\left( A \right){\cos ^{ - 1}}\left( {\dfrac{2}{3}} \right)$
$\left( B \right){\cos ^{ - 1}}\left( {\dfrac{5}{{\sqrt 3 }}} \right)$
$\left( C \right){\cos ^{ - 1}}\left( {\dfrac{5}{6}} \right)$
$\left( D \right){\cos ^{ - 1}}\left( {\dfrac{5}{{2\sqrt 3 }}} \right)$
Answer
233.1k+ views
Hint: Here the skier skies in a hemisphere radius are given. Its height from the smooth surface is given. At an angle, $\theta $ the skier leaves the hemisphere. Now using the given data draw a free body diagram. The force on a body is a centripetal force because the body undergoes circular motion. Equate the vertical and horizontal component of force with centripetal force and apply it to the work-energy theorem equation.
Formula used:
$F = \dfrac{{m{v^2}}}{R}$
Where $F$ s the centripetal force, $v$ is the velocity, $R$ is the radius of the hemisphere.
${\left( {KE} \right)_f} - {\left( {KE} \right)_i} = work$
Where ${\left( {KE} \right)_f},{\left( {KE} \right)_i}$ are the final and initial kinetic energy respectively
Complete step by step answer:
Free body diagrams will consist of a simplified version of the body. straight arrows are used for the force to point the direction they act on the body. The Moments are shown as curved arrows pointing in the direction they act on the body and they have a coordinate system.
The number of forces in a free body diagram depends on the problem and the assumptions made, common assumptions are neglecting air resistance and friction and assuming rigid bodies. All forces must balance to zero.
A force that makes a body move in a curved path is called centripetal force.
The vertical height is $\dfrac{R}{4} + R\left( {1 - \cos \theta } \right)$
Free body diagram is given below
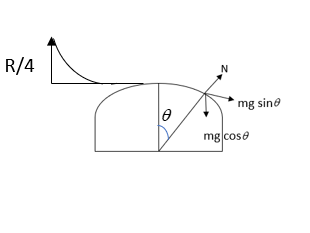
$mg\cos \theta - N = \dfrac{{m{v^2}}}{R}$
At the time when the skier leaves the hemisphere, the value of $N = 0$
$\Rightarrow g\cos \theta = \dfrac{{{v^2}}}{R}$
$\Rightarrow {\left( {KE} \right)_f} - {\left( {KE} \right)_i} = mg\left[ {\dfrac{R}{4} + R\left( {1 - \cos \theta } \right)} \right]$
$\Rightarrow \dfrac{1}{2}m{v^2} = mg\left[ {\dfrac{R}{4} + R\left( {1 - \cos \theta } \right)} \right]$
$\Rightarrow \dfrac{1}{2}m{v^2} = mg\left[ {\dfrac{R}{4} + R\left( {1 - \cos \theta } \right)} \right]$
$\Rightarrow \dfrac{3}{2}\cos \theta = \dfrac{5}{4}$
$\Rightarrow \cos \theta = \dfrac{5}{6}$
Hence option $\left( C \right)$ is the right option.
Note: If the body is moving then resultant forces and moments can be non-zero. A force that makes a body move in a curved path is called centripetal force. Centripetal force is directed towards the center and it acts on a body executing circular motion. In the Free body, diagram force is shown as straight-arrow pointing at the direction where force at.
Formula used:
$F = \dfrac{{m{v^2}}}{R}$
Where $F$ s the centripetal force, $v$ is the velocity, $R$ is the radius of the hemisphere.
${\left( {KE} \right)_f} - {\left( {KE} \right)_i} = work$
Where ${\left( {KE} \right)_f},{\left( {KE} \right)_i}$ are the final and initial kinetic energy respectively
Complete step by step answer:
Free body diagrams will consist of a simplified version of the body. straight arrows are used for the force to point the direction they act on the body. The Moments are shown as curved arrows pointing in the direction they act on the body and they have a coordinate system.
The number of forces in a free body diagram depends on the problem and the assumptions made, common assumptions are neglecting air resistance and friction and assuming rigid bodies. All forces must balance to zero.
A force that makes a body move in a curved path is called centripetal force.
The vertical height is $\dfrac{R}{4} + R\left( {1 - \cos \theta } \right)$
Free body diagram is given below

$mg\cos \theta - N = \dfrac{{m{v^2}}}{R}$
At the time when the skier leaves the hemisphere, the value of $N = 0$
$\Rightarrow g\cos \theta = \dfrac{{{v^2}}}{R}$
$\Rightarrow {\left( {KE} \right)_f} - {\left( {KE} \right)_i} = mg\left[ {\dfrac{R}{4} + R\left( {1 - \cos \theta } \right)} \right]$
$\Rightarrow \dfrac{1}{2}m{v^2} = mg\left[ {\dfrac{R}{4} + R\left( {1 - \cos \theta } \right)} \right]$
$\Rightarrow \dfrac{1}{2}m{v^2} = mg\left[ {\dfrac{R}{4} + R\left( {1 - \cos \theta } \right)} \right]$
$\Rightarrow \dfrac{3}{2}\cos \theta = \dfrac{5}{4}$
$\Rightarrow \cos \theta = \dfrac{5}{6}$
Hence option $\left( C \right)$ is the right option.
Note: If the body is moving then resultant forces and moments can be non-zero. A force that makes a body move in a curved path is called centripetal force. Centripetal force is directed towards the center and it acts on a body executing circular motion. In the Free body, diagram force is shown as straight-arrow pointing at the direction where force at.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




