Question

A rod of length l=1m leaving against a vertical wall is pulled at its lowest point A with a constant velocity $v = 4m{s^{ - 1}}$. In consequence, the rod rotates in the vertical plane. When the rod makes an angle $\theta = {37^0}$ with the vertical, find the angular velocity of the rod $({\text{in rad}}{{\text{s}}^{ - 1}})$

Answer 1

Hint: In this question let the distance from origin to point A on x-axis be x meters and the distance from origin to point B on y-axis be some y meters. Using Pythagoras theorem is triangle OAB (see figure), this will help forming a relationship between x, y and the length of the rod. Differentiate the equation formed with time and use the question constraints. This will help approach the solution to this problem.

Complete step-by-step solution -

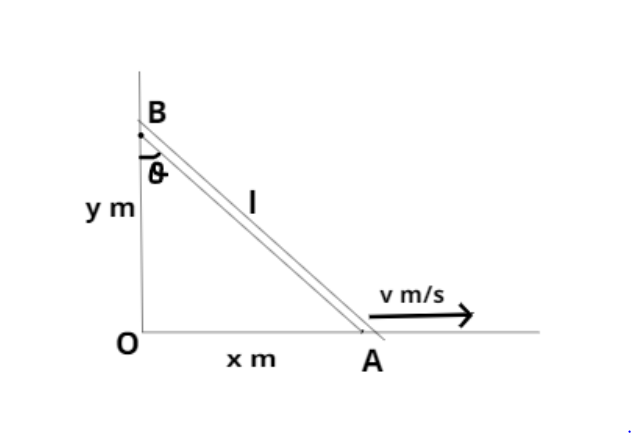
Let the A point of the rod is at the x-axis and the B point of the rod is on the y-axis.
Let OA = x and OB = y
The length of the rod is given which is $l = 1m$
So apply Pythagoras theorem in triangle OAB we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
$ \Rightarrow {\left( l \right)^2} = {\left( {\text{y}} \right)^2} + {\left( {\text{x}} \right)^2}$
$ \Rightarrow {\left( {\text{y}} \right)^2} + {\left( {\text{x}} \right)^2} = 1$
Now differentiate equation (1) w.r.t t we have,
As we know that the differentiation of constant is zero and $\dfrac{d}{{dt}}{t^n} = n{t^{n - 1}}$ so use this property we have,
$ \Rightarrow 2y\dfrac{{dy}}{{dt}} + 2x\dfrac{{dx}}{{dt}} = 0$
Now $\dfrac{{dx}}{{dt}}$ is the x direction velocity ${v_x}$and $\dfrac{{dy}}{{dt}}$ is y direction velocity ${v_y}$ so we have,
$ \Rightarrow 2y{v_y} + 2x{v_x} = 0$
Now simplify this we have,
$ \Rightarrow {v_y} = - \dfrac{x}{y}{v_x}$
Now it is given that the horizontal velocity ${v_x} = 4$m/s, so we have,
$ \Rightarrow {v_y} = - \dfrac{x}{y}\left( 4 \right)$
Now (x/y) is nothing but the slope of the rod which is $\tan \theta $ in the vertical plane.
$ \Rightarrow {v_y} = - 4\tan \theta $
Now the rod starts rotating when $\theta = {37^o}$in the vertical plane
$ \Rightarrow {v_y} = - 4\tan {37^o} = - 4\left( {0.75} \right) = - 3$m/s, (‘-’ sign indicates the direction of the velocity which is in the downward direction).
So the angular velocity $\left( \omega \right)$ of the rod is
$ \Rightarrow \omega = \dfrac{{{v_x} - {v_y}}}{l}$
Now substitute the values we have,
$ \Rightarrow \omega = \dfrac{{4\hat i - \left( { - 3\hat j} \right)}}{1}$, where $\hat i{\text{ and }}\hat j$ are the unit vectors in x and y direction respectively.
$ \Rightarrow \omega = 4\hat i + 3\hat j$
Now take the magnitude of the angular velocity we have,
$ \Rightarrow \left| \omega \right| = \left| {4\hat i + 3\hat j} \right| = \sqrt {{4^2} + {3^2}} = \sqrt {25} = 5$m/s.
So the angular velocity of the rod is 5 m/s.
So this is the required answer.

Note – Angular velocity that is $\omega $ is the rate of change of angular position of any rotating body. In general $\omega = \dfrac{{d\theta }}{{dt}}$. It is interesting to know that the average angular velocity of anybody that revolve around a fixed central point once every second is actually $2\pi /\sec $ because if it starts from say ${0^0}$ then it completes its ${360^0}$ to come back to the same point again thus the angular change in position is simply ${360^0}$.