Question

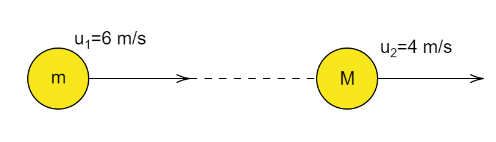
A particle of mass m moving with horizontal speed \[6{\text{ }}m/sec\] as shown in figure. If \[m < < M\;\] then for one dimensional elastic collision, the speed of lighter particles after collision will be ?

A. $2{\text{ }}m/\sec $ in original direction
B. $2{\text{ }}m/\sec $ opposite to the original direction
C. ${\text{4 }}m/\sec $ opposite to the original direction
D. ${\text{4 }}m/\sec $ in original direction

Answer 1

Hint:In this question, we are given the mass of two particles and their initial speed. We have to find the final speed of the particle with a smaller mass. Put the given values in the formula ${v_1} = \dfrac{{\left( {{m_1} - {m_2}} \right){u_1} + 2{m_2}{u_2}}}{{{m_1} + {m_2}}}$. As the mass of the first particle is very small then the mass of the second particle. We’ll put $m = 0$.

Formula used:
When two bodies collides (elastically) then the speeds are;
${v_1} = \dfrac{{\left( {{m_1} - {m_2}} \right){u_1} + 2{m_2}{u_2}}}{{{m_1} + {m_2}}}$, ${v_2} = \dfrac{{\left( {{m_2} - {m_1}} \right){u_2} + 2{m_1}{u_1}}}{{{m_1} + {m_2}}}$
Here, ${m_1},{m_2}$ and ${u_1},{u_2}$ are the masses and initial speed of both the bodies respectively.

Complete step by step solution:
Given that,
Mass of the particle $1$, ${m_1} = m$
Mass of the particle $2$, ${m_2} = M$
Initial speed of the particle $1$, ${u_1} = 6{\text{ }}m/s$
Initial speed of the particle $2$, ${u_2} = 4{\text{ }}m/s$
The nature of collision is elastic. Therefore, the final speed of the particle $1$ will be;
${v_1} = \dfrac{{\left( {{m_1} - {m_2}} \right){u_1} + 2{m_2}{u_2}}}{{{m_1} + {m_2}}}$
Substitute all the given values in the above formula,
${v_1} = \dfrac{{\left( {m - M} \right)\left( 6 \right) + 2\left( M \right)\left( 4 \right)}}{{m + M}}$
${v_1} = \dfrac{{\left( {m - M} \right)\left( 6 \right) + 8M}}{{m + M}}$
As, \[m < < M\;\] put $m = 0$
It implies that, ${v_1} = \dfrac{{2M}}{M}$
${v_1} = 2{\text{ }}m/\sec $
Now, the speed is positive. Therefore, it will move in the original direction.

Hence, option A is the correct answer i.e., $2{\text{ }}m/\sec $ in the original direction.

Note: When a system has an elastic collision then there is no net kinetic energy loss as a result of the collision. Momentum and kinetic energy are preserved in elastic collisions. When kinetic energy is lost, an inelastic collision happens. In an inelastic collision, the system's momentum is preserved, but its kinetic energy is not.