Question

A particle is moving along a circular path with a constant speed of \[10m{s^{ - 1}}\]. What is the magnitude of the change in velocity of the particle, when it moves through an angle of $60$ around the centre of the circle?
(A) $0$
(B) $10m/s$
(C) $10\sqrt 3 m/s$
(D) $10\sqrt 2 m/s$

Answer 1

Hint The particle is moving in a circular path at a constant speed. When the particle moves around the centre of the circle through an angle of ${60^ \circ }$the velocity of the particle changes. We have to find the change in the velocity of the particle.

Complete Step by step solution
The change in angle can be represented as follows:

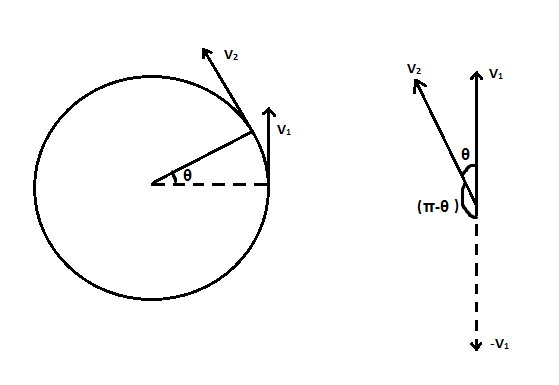
The velocity of the particle will be different in two different positions, let the velocities be ${v_1}$ and ${v_2}$. Since the velocities are vector quantities, the change in velocity of the particle can be written as,
$\Delta v = \left| {\overrightarrow {{v_2}} - \overrightarrow {{v_1}} } \right|$
Using the parallelogram method of vector addition, we have to find the resultant vector of $\overrightarrow {{v_2}} $and \[ - \overrightarrow {{v_1}} \].
$\left| {\Delta v} \right| = \sqrt {v_1^2 + v_2^2 + 2{v_1}{v_2}\cos \left( {\pi - \theta } \right)} $
It is given that, the magnitude of $\overrightarrow {{v_1}} $and $\overrightarrow {{v_2}} $are the same,
i.e.
$\overrightarrow {\left| {{v_1}} \right|} = \overrightarrow {\left| {{v_2}} \right|} = v = 10m/s$
Substituting this the equation for the change in velocity, we get
$\left| {\Delta v} \right| = \sqrt {{v^2} + {v^2} + 2{v^2}\cos \left( {\pi - \theta } \right)} $
We know that, $\cos \left( {\pi - \theta } \right) = - \cos \theta $
Substituting, we get
$\left| {\Delta v} \right| = \sqrt {{v^2} + {v^2} - 2{v^2}\cos \theta } $
This can be written as,
$\left| {\Delta v} \right| = \sqrt {2{v^2}} \times \sqrt {1 - \cos \theta } $
We know that, $1 - \cos \theta = 2{\sin ^2}\dfrac{\theta }{2}$
Substituting, we get
$\left| {\Delta v} \right| = \sqrt {2{v^2}} \times \sqrt {2{{\sin }^2}\dfrac{\theta }{2}} $
Canceling the squares and square root, this can be written as,
$\left| {\Delta v} \right| = 2v\sin \dfrac{\theta }{2}$
We know that,
$v = 10m/s$ and $\theta = {60^ \circ }$
Substituting, we get
$\left| {\Delta v} \right| = 2 \times 10 \times \sin \dfrac{{60}}{2}$
$ \Rightarrow \left| {\Delta v} \right| = 2 \times 10 \times \dfrac{1}{2} = 10m/s$

Therefore, the answer is Option (B): $10m/s$

Additional Information
The parallelogram law of vector addition is used to find the resultant vector of two vectors. According to which if we represent the direction and magnitude of any two vectors as the two sides of a parallelogram that are adjacent. Then the resultant vector is given by the diagonal drawn from the point where the two sides join.

Note
In a circular motion, the velocity will not be constant even when the particle is moving at a constant speed. This is because in a circular motion even though the magnitude is the same the direction of motion of the particle is always changing. The direction of velocity will be tangential to the position of the particle in a circular motion.