Question

A diverging lens of f=20cm and a converging mirror f=10cm are placed 5cm apart coaxially where shall an object be placed so that object and its real image coincide?
A. 60CM away from the lens
B. 15cm away from the lens
C. 20cm away from the lens
D. 45 cm away from the lens

Answer 1

Hint: First we have to draw the figure of both the mirrors and lens after that we use the simple rule of converging mirror and that is when we place object at center of the curvature of converging or concave mirror than image will produced at the center of the curvature with the same height by using this rule we will find where shall we place object.
Formula used:
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
v = distance of image from the lens
u = distance of the object from the mirror
f = focal length of the mirror

Complete answer:

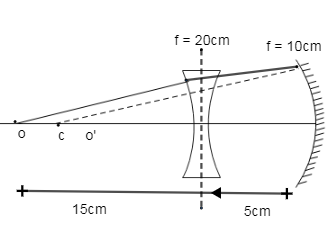
$\to $ Now assume that object is placed at a distance of y so that formula for the lens is given by
$\dfrac{1}{v}-\dfrac{1}{y}=\dfrac{1}{f}$
$\to $ Now substituting value of f for the lens we get
$\dfrac{1}{v}-\dfrac{1}{y}=\dfrac{1}{-20}....\left( 1 \right)$
$\to $In concave lens focal length will be negative (-ve).
$\to $Now suppose the image produced by the lens is at the center of the curvature in the concave mirror.
Now,
$\begin{align}
  & c=2\times 10 \\
 & c=20cm \\
\end{align}$
$\to $Now both lens and mirror are 5cm apart so the distance of the center of the curvature is
$\begin{align}
  & =20-5 \\
 & =15cm \\
\end{align}$
$\to $ Now if we assume that the image produced by the reflection is at the center of the curvature then the image produced by the reflection of the mirror is also at the center of the curvature.
$\to $Now it is again refract from point c so we can say that image distance from the lens is
$v=-15cm$
$\to $Now substitute value of the v in equation (1) we get
$\begin{align}
  & \Rightarrow -\dfrac{1}{15}-\dfrac{1}{7}=-\dfrac{1}{20} \\
 & \Rightarrow -\dfrac{1}{y}=-\dfrac{1}{20}+\dfrac{1}{15} \\
 & \Rightarrow \dfrac{1}{y}=\dfrac{1}{20}-\dfrac{1}{15} \\
 & \Rightarrow \dfrac{1}{y}=\dfrac{-5}{300} \\
 & \Rightarrow \dfrac{1}{y}=-\dfrac{1}{60} \\
 & \Rightarrow y=-60cm \\
\end{align}$
Therefore we can say that the object should be placed at 60cm from the left side of the lens to produce an image that coincides with the object.

Hence the correct option is (A) 60cm away from the lens.

Note:
When we are putting values from the left side of the lens all values should be taken with the negative sign. Otherwise it can lead us to wrong solution of this type of question