Question

(a) Define wave-front. Use Huygens’s principle to verify the laws of refraction.
(b) How is linearly polarized light obtained by the process of scattering of light?
Find the Brewster angle for the air-glass interface, when the refractive index of glass = 1.5.

Answer 1

Hint:In this problem, we have to define the wavefront which is well explained using Hygen’s principle. Also, we have to use the Huygens principle to verify the laws of refraction. One thing to note about refraction is there includes a change of medium and hence such speed of wave changes.Linearly polarized light literally means polarized in one direction and there are many ways of obtaining such a light. When we talk about polarization, we mean something related to fields and their directions.

Complete step by step answer:
Huygens’s principle in optics states that all points of a wavefront of light in vacuum or transparent medium are in the same phase.
(a) Wavefront: A wavefront is defined as the laws of all points of the medium which vibrate in the same phase.

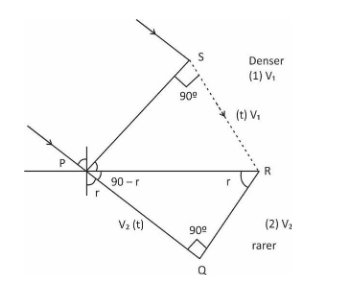
By using Huygens’s principle,
\[\Rightarrow {{V}_{2}}>{{V}_{1}}\]
In\[\Delta PRS\],
\[\Rightarrow \sin i=\dfrac{{{v}_{1}}t}{PR}\] … (1)
In\[\Delta PQR\],
\[\Rightarrow \sin \,\,r\,\,=\dfrac{{{v}_{2}}\left( t \right)}{PR}\] … (2)
From (1) and (2)
\[\Rightarrow \dfrac{\sin \,\,i}{\sin \,\,r}=\dfrac{{{v}_{1}}}{{{v}_{2}}}\] … (6)
\[\Rightarrow {{v}_{1}}=\dfrac{c}{{{n}_{1}}}\] … (3) (\[{{n}_{1}}\] – refractive index median)
\[\Rightarrow {{v}_{2}}=\dfrac{C}{{{n}_{2}}}\] … (4)
From (3) and (4)
\[\Rightarrow \dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{{{n}_{2}}}{{{n}_{1}}}\] … (5)
From (5) and (6)
\[\Rightarrow \dfrac{\sin \,\,i}{\sin \,\,r}=\dfrac{{{n}_{1}}}{{{n}_{1}}}\]
(b) When unpolarised light hits a reflective surface, the vertically polarized aspects are reflected into the surface. The horizontally polarized aspects are reflected off the surface and the light is now perceived as partially polarized.When light is reflected, there is an angle at which this light is completely polarized. This is called Brewster’s angle which is named after the Scottish physicist who discovered this law.
As per Brewster’s rule = \[{{\tan{i}}_{f}}\]
\[\Rightarrow 1.5\,\,=\,\,{{\tan{i}}_{f}}\]
\[\Rightarrow \therefore {{\tan{i}}_{f}}={{\tan }^{-1}}\left( \dfrac{3}{2} \right)=56.3{}^\circ \]

Note: While using Snell’s law of refraction and while specifically writing the refractive index when a light wave moves from one medium to another we have to bear this in our mind that the refractive index is written as the ratio of the given two mediums and in the numerator, we have to write the index of that medium in which the light was travelling and in the denominator the index of the medium in which the light enters.
-When talking about polarization in terms of Brewster law, there are two lights after the incident. One is reflected into the same medium and one is refracted in the other medium. Both the reflected and refracted lights are always perpendicular and if they are not you cannot apply Brewster’s law