Question

A circle $'S'$ is described on the focal chord of the parabola ${{y}^{2}}=4x$ as diameter. If the focal chord is inclined at an angle of $45{}^\circ $ with an axis of $x$ , then
 which of the following is/are true?
(A) Radius of the circle is $4.$
(B) Centre of the circle is $\left( 3,2 \right)$
(C) The line $x+1=0$ touches the circle
(D) The circle ${{x}^{2}}+{{y}^{2}}+2x-6y+3=0$ is orthogonal to $'S'$

Answer 1

Hint: Consider the directrix of the circle touching the parabola as $x+1=0$ and
 frame the equation of the circle.

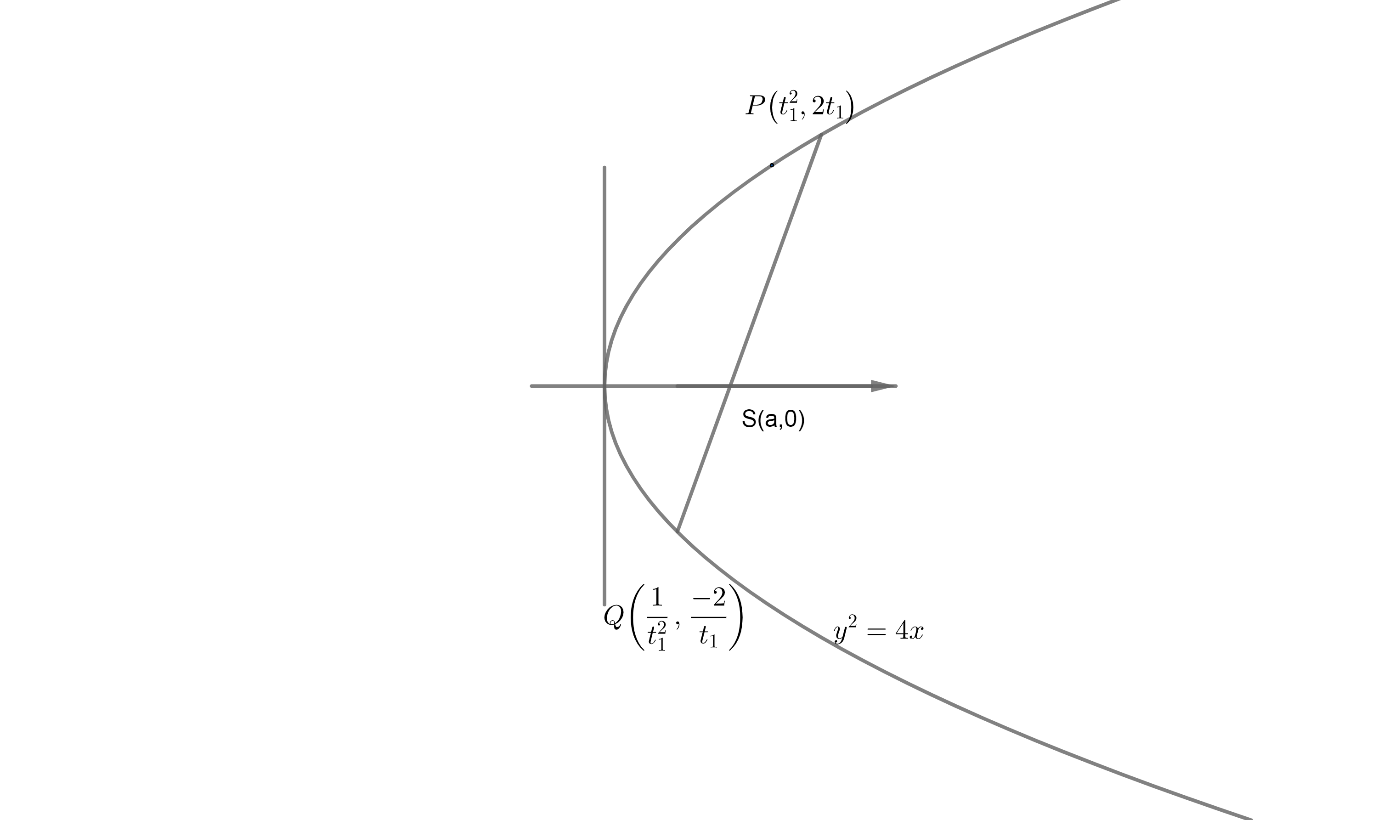
From the figure, it shows the parabola ${{y}^{2}}=4x$
Let $P$ and $Q$ be the extremities of the focal chord.
Where $P$is $\left( {{t}_{1}}^{2},2{{t}_{1}} \right)$
$Q$ is $\left( \dfrac{1}{{{t}_{1}}^{2}},\dfrac{-2}{{{t}_{1}}} \right)$
And it's given in the question that the focal chord $PQ$ is inclined at an angle of $45{}^\circ
 $ with $x-axis$.
The directrix of the circle touches the parabola
i.e. directrix of circle $\Rightarrow x+1=0...................\left( 1 \right)$
Now the equation of the circle can be written as from $P$and $Q$
\[\begin{align}
  & P\left( \underset{{{X}_{1}}}{\mathop{{{t}_{1}}^{2}}}\,,\underset{{{Y}_{1}}}{\mathop{2{{t}_{1}}}}\,
 \right)\text{ and }Q\left( \dfrac{1}{\underset{{{X}_{2}}}{\mathop{{{t}_{1}}^{2}}}\,},-\dfrac{2}{\underset{{{Y}_{2}}}{\mat
hop{{{t}_{2}}}}\,} \right) \\
 & \Rightarrow \left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left(
 y-{{y}_{2}} \right)=0 \\
 & \Rightarrow \left( x-{{t}_{1}}^{2} \right)\left( x-\dfrac{1}{{{t}_{1}}^{2}} \right)+\left( y-2{{t}_{1}} \right)\left( y+\dfrac{2}{{{t}_{1}}} \right)=0 \\
\end{align}\]
Opening the brackets and simplifying it
$\begin{align}
  & {{x}^{2}}-\dfrac{x}{{{t}_{1}}^{2}}-x{{t}_{1}}^{2}+1+{{y}^{2}}+\dfrac{2y}{{{t}_{1}}}-2y{{t}_{1}}-4=0
 \\
 & \Rightarrow {{x}^{2}}-\dfrac{x}{{{t}_{1}}^{2}}-x{{t}_{1}}^{2}+{{y}^{2}}+\dfrac{2y}{{{t}_{1}}}-2y{{t}_{1}}-3=0 \\
 & \Rightarrow {{x}^{2}}-\left( {{t}_{1}}^{2}+\dfrac{1}{{{t}_{1}}^{2}} \right)x+{{y}^{2}}-2\left[
 {{t}_{1}}-\dfrac{1}{{{t}_{1}}} \right]y-3=0...........\left( 2 \right) \\
\end{align}$
Let’s take the slope of focal chord $PQ=1$
We know the equation of slope $\Rightarrow \dfrac{y-{{y}_{1}}}{x-{{x}_{1}}}=\dfrac{2a}{{{y}_{1}}}$
This is the equation of the chord of the parabola ${{y}^{2}}=4ax$
Here $\left( x,y \right)$ can be taken as $\left( {{t}_{1}}^{2},2{{t}_{1}} \right)$
$\left( {{x}_{1}},{{y}_{1}} \right)$ can be taken as $\left(
 \dfrac{1}{{{t}_{1}}^{2}},\dfrac{-2}{{{t}_{1}}} \right)$
$\dfrac{2a}{{{y}_{1}}}=1$ [i.e. slope of focal chord is taken as $1$ ]
i.e. $\tan 45{}^\circ =1$
Substituting the coordinates $\left( {{t}_{1}}^{2},2{{t}_{1}} \right)$ and $\left(
 \dfrac{1}{{{t}_{1}}^{2}},\dfrac{-2}{{{t}_{1}}} \right)$
in the equation of slope
$\dfrac{y-{{y}_{1}}}{x-{{x}_{1}}}=1\Rightarrow \dfrac{2{{t}_{1}}\left( \dfrac{-2}{{{t}_{1}}}
 \right)}{{{t}_{1}}^{2}-\dfrac{1}{{{t}_{1}}^{2}}}=1\Rightarrow \dfrac{2\left(
 {{t}_{1}}+\dfrac{1}{{{t}_{1}}} \right)}{{{t}_{1}}^{2}-\dfrac{1}{{{t}_{1}}^{2}}}=1$
We know the equation ${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$
\[\begin{align}
  & \dfrac{2\left( {{t}_{1}}-\dfrac{1}{{{t}_{1}}} \right)}{{{t}_{1}}^{2}-\dfrac{1}{{{t}_{1}}^{2}}}=1
 \\
 & \Rightarrow \dfrac{2\left( {{t}_{1}}+\dfrac{1}{{{t}_{1}}} \right)}{\left(
 {{t}_{1}}-\dfrac{1}{{{t}_{1}}} \right)\left( {{t}_{1}}+\dfrac{1}{{{t}_{1}}} \right)}=1 \\
\end{align}\]
By cancelling the like terms we get
$\dfrac{2}{{{t}_{1}}-\dfrac{1}{{{t}_{1}}}}=1$
$\therefore $ By cross multiplying we get
${{t}_{1}}-\dfrac{1}{{{t}_{1}}}=2$
Multiplying throughout by ${{t}_{1}}$
${{t}_{1}}^{2}-1-2{{t}_{1}}=0\Rightarrow {{t}_{1}}^{2}-2{{t}_{1}}-1=0..............\left( 3 \right)$
By solving the equation using quadratic equation which is of form
$a{{x}^{2}}+bx+c=0$
Comparing the general equation with equation $\left( 3 \right)$
$a=1,b=-2\text{ and }c=-1$
Substituting them in the quadratic formula$\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
$\begin{align}
  & \dfrac{\left( -2 \right)\pm \sqrt{{{\left( -2 \right)}^{2}}-4\times 1\times \left( -1
 \right)}}{2\times 1}=\dfrac{2\pm \sqrt{4+4}}{2}=\dfrac{2\pm \sqrt{8}}{2} \\
 & =\dfrac{2\pm 2\sqrt{2}}{2}=1\pm \sqrt{2} \\
\end{align}$
i.e. we get the roots as $\left( 1+\sqrt{2} \right)$ and $\left( 1-\sqrt{\sqrt{2}} \right)$
We neglect $\left( 1+\sqrt{2} \right)$as the root of the solution
$\therefore {{t}_{1}}=1+\sqrt{2}$
By substituting the value of ${{t}_{1}}=1+\sqrt{2}$ to find the radius of the circle, we get a
 rather big equation which does not fit to the option provided in the question.
$\therefore $ The only correct option is $\left( c \right)$ the line $x+1=0$ touches the circle.

Correct option is C.

Note: (i) Here the parametric coordinates of the parabola $P$ is $\left( a{{t}^{2}},2at \right)$
Here $a=1$ $\therefore $ the coordinates of $P$are $\left( {{t}^{2}},2t \right),a>0$
(ii) A common mistake that can happen here is taking ${{t}^{2}}-2{{t}_{1}}+1=0$ instead of
 ${{t}^{2}}-2{{t}_{1}}-1=0$
Because of this we get the value of ${{t}_{1}}=1$
And thus the radius will be 4 .
Because of this you might mistakenly choose option A instead of option C .