Question

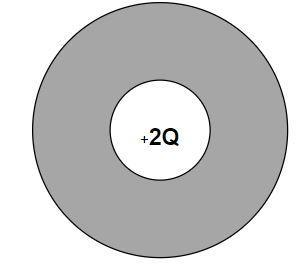
A charge of $ + 2Q$ resides inside of a conducting sphere with a hollow center. If the net charge on the conducting sphere is $ + 5Q$ , what is the amount of charge on the outer surface of the conduction sphere?

(A) $2Q$
(B) $3Q$
(C) $5Q$
(D) $7Q$

Answer 1

Hint:Compare the given sphere with the Gaussian surface and apply the Gaussian formula in it. Find the charge in the inside the sphere, on the sphere and outside of the sphere. The Gaussian law is only applicable to the closed surfaces.

Complete step by step solution:

The charge inside the hollow sphere is $ + 2Q$

Total charge on the conducting sphere is $ + 5Q$

The gauss’s law is used to solve this question. The gauss law states that the electric field on the closed surface is directly proportional to the charge in which the closed surface encloses. The given hollow sphere represents the Gaussian surface with the inner charge. Since the charge of $ + 2Q$ is placed inside the hollow sphere, by the application of the gauss law, the electric field inside the closed hollow sphere is zero. The electric field on the closed surface is given by the $E = \dfrac{{kQ}}{{{r^2}}}$ . It also states that the more charges are placed outside the Gaussian sphere. It is obtained by the sum of the electric field due to the charge in the small sphere and the large sphere.
$ = 5Q + 2Q$
$ = 7Q$

Thus the option (D) is correct.

Note:In a closed loop, while the material conducts the electricity, all the electrons come and stay on the external surface and no charge will be inside the surface. This is because the conducting material has the free electrons in it which is very loosely held by the nucleus moving out to the surface.