Question

A body falling freely from a given height $H$ hits an inclined plane in its path at a height. As a result of this impact the direction of the velocity of the body becomes horizontal. For what value of $\left( {\dfrac{h}{H}} \right)$ body will take a maximum time to reach the ground.
A) $\dfrac{1}{3}$
B) $\dfrac{1}{2}$
C) $\dfrac{2}{5}$
D) $\dfrac{2}{3}$

Answer 1

Hint: To find the answer for the given solution, first we need to draw a reference diagram and then we should find the total time taken by the body to fall. From this we can calculate the value of $\left( {\dfrac{h}{H}} \right)$ in which the body will take a maximum time to reach the ground.

Complete step by step solution:

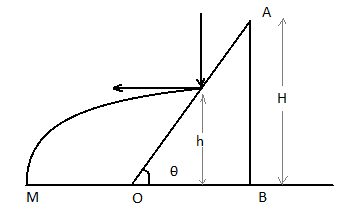
From above diagram the body which falls from height $H$ from the point $B$ from $h$ height above the ground. The path of the body after striking it will be like a parabola.
Then the time taken by the body to fall A to B is ${t_1}$.
$ \Rightarrow \left( {H - h} \right) = \dfrac{1}{2}g{t_1}^2$
$ \Rightarrow {t_1} = \sqrt {\dfrac{{2\left( {H - h} \right)}}{g}} $
The time taken by the body which falls from B to M is ${t_2}$.
$ \Rightarrow h = \dfrac{1}{2}g{t_2}^2$
$ \Rightarrow {t_2} = \sqrt {\dfrac{{2h}}{g}} $
Then the total time taken by the body to fall,
$ \Rightarrow T = {t_1} + {t_2}$
$ \Rightarrow T = \sqrt {\dfrac{{2(H - h)}}{g}} + \sqrt {\dfrac{{2h}}{g}} $
By taking the common elements out then the equation is,
$ \Rightarrow T = \sqrt {\dfrac{2}{g}[(H - h)^{1/2} +{h}^{1/2}]} $
If the body reaches the maximum height then $\dfrac{{dt}}{{dh}} = 0$
We need to differentiate the above equation with respect to $h$we get,
$\dfrac{1}{2}{(H - h)^{\dfrac{{ - 1}}{2}}}( - 1) + \dfrac{1}{2}{h^{\dfrac{{ - 1}}{2}}} = 0$
$ \Rightarrow H - h = h$
$ \Rightarrow H = h + h$
$ \Rightarrow H = 2h$
$ \Rightarrow \dfrac{h}{H} = \dfrac{1}{2}$
Then the value of $\dfrac{h}{H}$ in which the body takes the maximum time to reach the ground is $\dfrac{1}{2}$.

Therefore the option (B) is correct.

Note: The above problem is based on kinematics that is motion in a straight line. The kinematics are used in day to day life everywhere, kinematics is a kind of mechanism in which dynamics can concern the forces. The main application of the kinematics is used in astrophysics that is robotics, biomechanics and also in mechanical engineering. Because it is used to describe the motion of the system to joint parts.