Question

(a) An electric dipole of dipole moment $\vec p$ consists of point charge $ + q$ and $ - q$ separately by a distance $2a$ apart. Deduce the expression for the electric field $\vec E$ due to the dipole at a distance x from the center of the dipole on its axial line in terms of the dipole moment $\vec p$. Hence show that the limit $X > > a$, $\vec E \to \dfrac{{2\vec p}}{{4\pi {\varepsilon _0}{x^3}}}$.

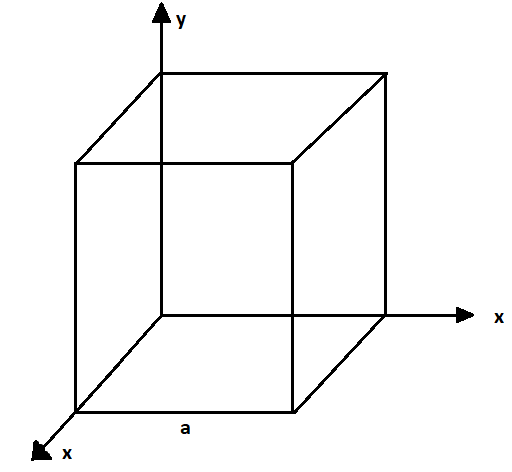
(b) Given the electric field in the region $\vec E = 2x\hat i$, find the net electric flux through the cube and the charge enclosed by it.

Answer 1

Hint: Recall the formula for the electric field at a point due to point charge and also the formula for the electric field on the axial line of an electric dipole. Also keep in mind what is the electric flux? What is its formula? And also its nature and characteristics.

Complete step by step solution:
(a) Electric field on axial line of an electric dipole is given by,

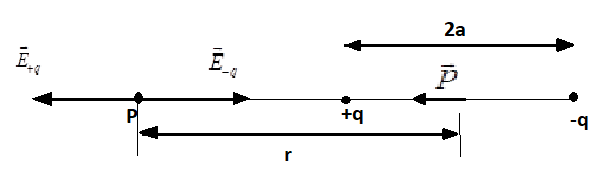
Let us assume that the P is the point at a distance r from the center of the given dipole on the side of charge –q.
Now, the formula for the electric field at point P due to –q is given by,
${E_{ - q}} = - \dfrac{q}{{4\pi {\varepsilon _0}{{(r - a)}^2}}}\hat p$
Now, the electric field at point P due to +q is given by,
${E_{ - q}} = \dfrac{q}{{4\pi {\varepsilon _0}{{(r - a)}^2}}}\hat p$
Therefore, the total electric field at point P is,
$E = {E_{ + q}} + {E_{ - q}}$
$ \Rightarrow E = \dfrac{q}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{1}{{{{(r - a)}^2}}} - \dfrac{1}{{{{(r + a)}^2}}}} \right]\hat p$
\[ \Rightarrow E = \dfrac{q}{{4\pi {\varepsilon _0}}}\dfrac{{4ar}}{{{{({r^2} - {a^2})}^2}}}\hat p\]
At $r = x$, we have
\[ \Rightarrow E = \dfrac{q}{{4\pi {\varepsilon _0}}}\dfrac{{4ar}}{{{{({x^2} - {a^2})}^2}}}\hat p\]
In the question it is given the limit, so for $x > > a$,we get
$ \Rightarrow E = \dfrac{{4qa}}{{4\pi {\varepsilon _0}{x^3}}}$
On further solving, we get
$E = \dfrac{{2p}}{{4\pi {\varepsilon _0}{x^3}}}$
Hence, we got the desired result.

(b) The face of the cube that is perpendicular to the direction of x-axis, generates the flux. The face of the cube is parallel to the xy and xz plane and the electric field is parallel to the face, so the electric flux through them is zero.
Electric flux through the left face of the cube is given by,
${\phi _L} = {E_L}{a^2}\cos 180^\circ = 0$
Now, the electric flux through the right face of the cube is given by,
\[{\phi _R} = ({E_R})({a^2})\cos 0^\circ \]
On putting the value ${E_R} = 2a$, we get
$ \Rightarrow {\phi _R} = 2{a^3}$
So the net flux through the cube is given by $ \Rightarrow {\phi _R} = 2{a^3}$
And now the charge enclosed by the cube is given by,
\[\phi = \dfrac{{{q_{enclosed}}}}{{{\varepsilon _0}}}\]
Put the value for the flux from above in this equation, we get
\[ \Rightarrow 2{a^3} = \dfrac{{{q_{enclosed}}}}{{{\varepsilon _0}}}\]
On further solving, we get the charge enclosed by the cube,
${q_{enclosed}} = 2{a^3}{\varepsilon _0}$

Therefore, we get the net flux as $ {\phi _R} = 2{a^3}$ And, the charge enclosed by the cube as ${q_{enclosed}} = 2{a^3}{\varepsilon _0}$.

Note: Always remember that the electric flux is proportional to the number of electric field lines. It is basically defined as the measure of flow of the electric field through a given area. Also remember that the electric flux through a closed surface does not depend on the shape or size of the surface.