
A $2m$ wide truck is moving with a uniform speed ${v_0} = 8m{s^{ - 1}}$ along a straight horizontal road. A pedestrian starts to cross the road with a uniform speed v, when the truck is $4m$ away from him. The minimum value of v so that he cross the road safely is
(A) $2.62m{s^{ - 1}}$
(B) $4.6m{s^{ - 1}}$
(C) $3.57m{s^{ - 1}}$
(D) $1.414m{s^{ - 1}}$
Answer
232.8k+ views
Hint A truck is moving at a uniform speed along a straight line. At the same time a pedestrian started crossing the road with a uniform speed. We have to find the minimum velocity required to cross the road without getting hit by the truck which is at a particular distance from the person.
Complete step by step answer
A truck which is $2m$ wide is moving with a uniform velocity along a straight line. At the same time a pedestrian starts to cross the road. Let us assume that person is in the position C, he wants to cross the road and reach point B. the distance between the truck and the person is 4m. Let A be the point parallel to the person at C at a distance $2m$. With this draw a triangle joining the points A, B and C. Then AC is $2m$, let AB be x and let BC be y.
Let us make a diagram using above discussion,
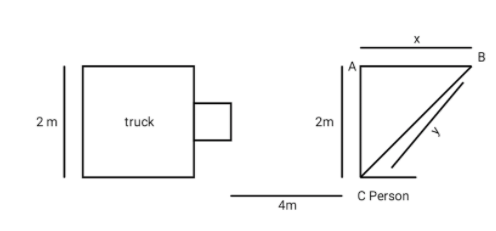
The distance between the truck and the point B, $s = 4 + x$
The truck moves with the velocity, ${v_T} = 8m{s^{ - 1}}$
Let us take the triangle ABC, it is a right angled triangle. According to the Pythagoras theorem,$ \Rightarrow y = \sqrt {{x^2} + {2^2}} $
$y = \sqrt {{x^2} + 4} $
The distance between the person at the point C and the point B (other side), $y = \sqrt {{x^2} + 4} $
The person moves with the velocity ${v_P} = ?$
Velocity: the velocity is determined by the rate of change of displacement. I.e. displacement by time taken.
$ \Rightarrow v = \dfrac{d}{t}$
This can be rewritten as
$ \Rightarrow t = \dfrac{d}{v}$
V is the velocity
d is the displacement
t is the time taken
The time taken by the truck to reach the point B is given by
$ \Rightarrow t = \dfrac{d}{v}$
$ \Rightarrow {t_T} = \dfrac{{4 + x}}{8}{\text{ }} \to {\text{1}}$
The time taken by the person to reach the point B is given by
$ \Rightarrow t = \dfrac{d}{v}$
$ \Rightarrow {t_P} = \dfrac{{\sqrt {{x^2} + 4} }}{{{v_p}}}{\text{ }} \to {\text{2}}$
To cross the road safely without getting hit by the truck the time taken by the truck to reach the point B should be equal to the time taken by the person to reach the point B
So, equating 1 and 2
$ \Rightarrow \dfrac{{4 + x}}{8} = \dfrac{{\sqrt {{x^2} + 4} }}{{{v_p}}}$
$ \Rightarrow {v_p} = \dfrac{{\sqrt {{x^2} + 4} }}{{4 + x}} \times 8{\text{ }} \to {\text{3}}$
To get minimum velocity of the person
$ \Rightarrow \dfrac{{dv}}{{dt}} = 0$
$ \Rightarrow \dfrac{d}{{dt}}\dfrac{{\sqrt {{x^2} + 4} }}{{4 + x}} \times 8 = 0$
\[ \Rightarrow 8\left( {\dfrac{{\left( {4 + x} \right) \times \dfrac{x}{{\sqrt {{x^2} + 4} }} - \sqrt {{x^2} + 4} }}{{{{\left( {x + 4} \right)}^2}}}} \right) = 0\]
\[ \Rightarrow 8\left( {\dfrac{{\left( {4 + x} \right) \times \dfrac{{x - \left( {{x^2} + 4} \right)}}{{\sqrt {{x^2} + 4} }}}}{{{{\left( {x + 4} \right)}^2}}}} \right) = 0\]
\[ \Rightarrow 8\left( {\dfrac{{\left( {x + 4} \right)x - \left( {{x^2} + 4} \right)}}{{\sqrt {{x^2} + 4} }}} \right) = 0\]
\[ \Rightarrow \left( {x + 4} \right)x - \left( {{x^2} + 4} \right) = 0\]
\[ \Rightarrow {x^2} + 4x - {x^2} - 4 = 0\]
\[ \Rightarrow 4x - 4 = 0\]
\[ \Rightarrow 4\left( {x - 1} \right) = 0\]
\[ \Rightarrow \left( {x - 1} \right) = 0\]
\[ \Rightarrow x = 1\]
Substitute the value of x in equation 3
$ \Rightarrow {v_p} = \dfrac{{\sqrt {{x^2} + 4} }}{{4 + x}} \times 8$
$ \Rightarrow {v_p} = \dfrac{{\sqrt {{1^2} + 4} }}{{4 + 1}} \times 8$
$ \Rightarrow {v_p} = \dfrac{{\sqrt 5 }}{5} \times 8 = \dfrac{8}{{\sqrt 5 }}$
$ \Rightarrow {v_p} = 3.57m{s^{ - 1}}$
The minimum value of velocity required to cross the road safely is $3.57m{s^{ - 1}}$
Hence the correct answer is option (C) $3.57m{s^{ - 1}}$
Note We have used Pythagorean Theorem to solve this question. Pythagorean’s theorem is defined as the square of the hypotenuse is equal to the sum of squares of the other two sides. We should clearly understand the position of the objects (truck and the person) mentioned in the question to solve this problem.
Complete step by step answer
A truck which is $2m$ wide is moving with a uniform velocity along a straight line. At the same time a pedestrian starts to cross the road. Let us assume that person is in the position C, he wants to cross the road and reach point B. the distance between the truck and the person is 4m. Let A be the point parallel to the person at C at a distance $2m$. With this draw a triangle joining the points A, B and C. Then AC is $2m$, let AB be x and let BC be y.
Let us make a diagram using above discussion,

The distance between the truck and the point B, $s = 4 + x$
The truck moves with the velocity, ${v_T} = 8m{s^{ - 1}}$
Let us take the triangle ABC, it is a right angled triangle. According to the Pythagoras theorem,$ \Rightarrow y = \sqrt {{x^2} + {2^2}} $
$y = \sqrt {{x^2} + 4} $
The distance between the person at the point C and the point B (other side), $y = \sqrt {{x^2} + 4} $
The person moves with the velocity ${v_P} = ?$
Velocity: the velocity is determined by the rate of change of displacement. I.e. displacement by time taken.
$ \Rightarrow v = \dfrac{d}{t}$
This can be rewritten as
$ \Rightarrow t = \dfrac{d}{v}$
V is the velocity
d is the displacement
t is the time taken
The time taken by the truck to reach the point B is given by
$ \Rightarrow t = \dfrac{d}{v}$
$ \Rightarrow {t_T} = \dfrac{{4 + x}}{8}{\text{ }} \to {\text{1}}$
The time taken by the person to reach the point B is given by
$ \Rightarrow t = \dfrac{d}{v}$
$ \Rightarrow {t_P} = \dfrac{{\sqrt {{x^2} + 4} }}{{{v_p}}}{\text{ }} \to {\text{2}}$
To cross the road safely without getting hit by the truck the time taken by the truck to reach the point B should be equal to the time taken by the person to reach the point B
So, equating 1 and 2
$ \Rightarrow \dfrac{{4 + x}}{8} = \dfrac{{\sqrt {{x^2} + 4} }}{{{v_p}}}$
$ \Rightarrow {v_p} = \dfrac{{\sqrt {{x^2} + 4} }}{{4 + x}} \times 8{\text{ }} \to {\text{3}}$
To get minimum velocity of the person
$ \Rightarrow \dfrac{{dv}}{{dt}} = 0$
$ \Rightarrow \dfrac{d}{{dt}}\dfrac{{\sqrt {{x^2} + 4} }}{{4 + x}} \times 8 = 0$
\[ \Rightarrow 8\left( {\dfrac{{\left( {4 + x} \right) \times \dfrac{x}{{\sqrt {{x^2} + 4} }} - \sqrt {{x^2} + 4} }}{{{{\left( {x + 4} \right)}^2}}}} \right) = 0\]
\[ \Rightarrow 8\left( {\dfrac{{\left( {4 + x} \right) \times \dfrac{{x - \left( {{x^2} + 4} \right)}}{{\sqrt {{x^2} + 4} }}}}{{{{\left( {x + 4} \right)}^2}}}} \right) = 0\]
\[ \Rightarrow 8\left( {\dfrac{{\left( {x + 4} \right)x - \left( {{x^2} + 4} \right)}}{{\sqrt {{x^2} + 4} }}} \right) = 0\]
\[ \Rightarrow \left( {x + 4} \right)x - \left( {{x^2} + 4} \right) = 0\]
\[ \Rightarrow {x^2} + 4x - {x^2} - 4 = 0\]
\[ \Rightarrow 4x - 4 = 0\]
\[ \Rightarrow 4\left( {x - 1} \right) = 0\]
\[ \Rightarrow \left( {x - 1} \right) = 0\]
\[ \Rightarrow x = 1\]
Substitute the value of x in equation 3
$ \Rightarrow {v_p} = \dfrac{{\sqrt {{x^2} + 4} }}{{4 + x}} \times 8$
$ \Rightarrow {v_p} = \dfrac{{\sqrt {{1^2} + 4} }}{{4 + 1}} \times 8$
$ \Rightarrow {v_p} = \dfrac{{\sqrt 5 }}{5} \times 8 = \dfrac{8}{{\sqrt 5 }}$
$ \Rightarrow {v_p} = 3.57m{s^{ - 1}}$
The minimum value of velocity required to cross the road safely is $3.57m{s^{ - 1}}$
Hence the correct answer is option (C) $3.57m{s^{ - 1}}$
Note We have used Pythagorean Theorem to solve this question. Pythagorean’s theorem is defined as the square of the hypotenuse is equal to the sum of squares of the other two sides. We should clearly understand the position of the objects (truck and the person) mentioned in the question to solve this problem.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




