Question

\[2{{\cos }^{-1}}x={{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)\] is valid for all the values of x satisfying
(a) \[-1\le x\le 1\]
(b) \[0\le x\le 1\]
(c) \[\dfrac{1}{\sqrt{2}}\le x\le 1\]
(d) \[0\le x\le \dfrac{1}{\sqrt{2}}\]

Answer 1

Hint: We know that the range of \[{{\sin }^{-1}}2x\sqrt{1-{{x}^{2}}}\] is \[\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]\], so the same would be for \[2{{\cos }^{-1}}x\]. From this, find the range of \[{{\cos }^{-1}}x\] and then find the value of x for which it is true.

Complete step-by-step answer:
We are given an equation \[2{{\cos }^{-1}}x={{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)\]. We have to solve it and find all the values of x that satisfy this.
Let us consider the equation i.e. : \[2{{\cos }^{-1}}x={{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)\]
We know that the range of \[{{\sin }^{-1}}t\] is \[\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]\].
So, we also get the range \[{{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)\] as \[\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]\]
Or, \[\dfrac{-\pi }{2}\le {{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)\le \dfrac{\pi }{2}\]
Since, we know that \[2{{\cos }^{-1}}x={{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)\] then, \[2{{\cos }^{-1}}x\] will also have the same range as \[{{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)\]. So, we get,
\[\dfrac{-\pi }{2}\le 2{{\cos }^{-1}}x\le \dfrac{\pi }{2}\]
By dividing 2 in the above equation, we get,
\[\dfrac{\dfrac{-\pi }{2}}{2}\le \dfrac{2{{\cos }^{-1}}x}{2}\le \dfrac{\dfrac{\pi }{2}}{2}\]
Or, \[\dfrac{-\pi }{4}\le {{\cos }^{-1}}x\le \dfrac{\pi }{4}\]
Now, we will draw the graph of \[{{\cos }^{-1}}x\] to analyze the above inequality.

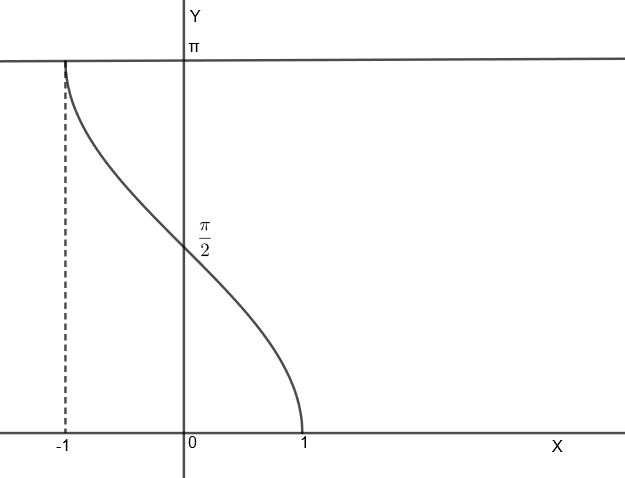
Since, we can see that the range of \[{{\cos }^{-1}}x\] is \[\left[ 0,\pi \right]\], so we will get the range of \[{{\cos }^{-1}}x\] in this question as, \[0\le {{\cos }^{-1}}x\le \dfrac{\pi }{4}\] because \[{{\cos }^{-1}}x\] cannot take negative values.
For \[{{\cos }^{-1}}x=0\], we get x = cos 0 = 1.
And for \[{{\cos }^{-1}}x=\dfrac{\pi }{4}\], we get \[x=\cos \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}\].
So, we get, \[\dfrac{1}{\sqrt{2}}\le x\le 1\].
Hence, option (c) is the right answer.

Note: In this question, we can also consider the graph of \[{{\cos }^{-1}}x\] to solve the inequality
\[0\le {{\cos }^{-1}}x\le \dfrac{\pi }{4}\]

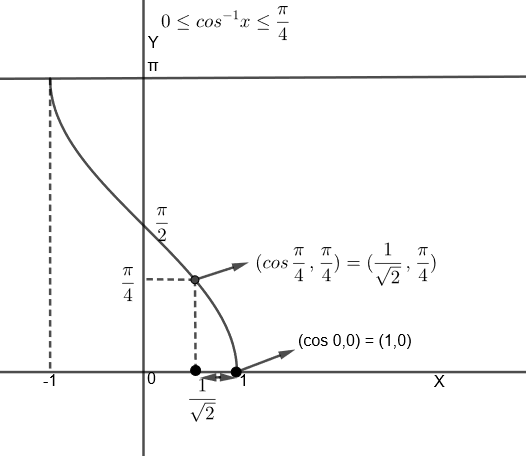
From the above graph, we can see that, when \[{{\cos }^{-1}}x\in \left[ 0,\dfrac{\pi }{4} \right]\], then \[x\in \left[ \dfrac{1}{\sqrt{2}},1 \right]\]. In questions involving the inverse trigonometric functions, take the special case of range and domain of the function.