
How many $176\Omega $ resistors (in parallel) are required to carry 5A in 220V line?
Answer
570.3k+ views
Hint: The net resistance for two resistors of resistances $\left( {{R}_{1}} \right)$and $\left( {{R}_{2}} \right)$connected in parallel is given by; \[\dfrac{1}{{{R}_{parallel}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}\], where the net resistance is \[\left( {{R}_{parallel}} \right)\]. Further, the Ohm’s law will also be used. The Ohm’s law is given by: $V=IR$.
Complete step by step solution:
Let’s find out how a parallel resistance circuit works. A parallel resistance circuit is made below.
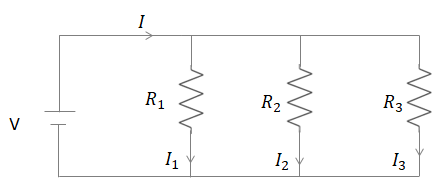
The voltage source is (V) and the net amount of current flowing through the circuit is (I). There are three resistances: \[\left( {{R}_{1}} \right)\], \[\left( {{R}_{2}} \right)\] and \[\left( {{R}_{3}} \right)\]connected in parallel to each other. The amount of current through each branch of resistor is given by: \[\left( {{I}_{1}} \right)\], \[\left( {{I}_{2}} \right)\] and \[\left( {{I}_{3}} \right)\].
The values of the individual amount of current through each resistance, can be found through the Ohm’s law: $V=IR\Rightarrow I=\dfrac{V}{R}$. Hence, the value \[\left( {{I}_{1}} \right)\]is: \[{{I}_{1}}=\dfrac{V}{{{R}_{1}}}\]. Similarly, the value of \[\left( {{I}_{2}} \right)\]is: \[{{I}_{2}}=\dfrac{V}{{{R}_{2}}}\] and the value of \[\left( {{I}_{3}} \right)\]is: \[{{I}_{3}}=\dfrac{V}{{{R}_{3}}}\]. Using the Kirchoff’s current law: $I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}$.
Hence, $I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}$ becomes: $I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}\Rightarrow \dfrac{V}{R}=\dfrac{V}{{{R}_{1}}}+\dfrac{V}{{{R}_{2}}}+\dfrac{V}{{{R}_{3}}}\Rightarrow \dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$.
Let’s consider a special case of the resistances connected in parallel. In this case, the resistances are of same value, that is: $\dfrac{1}{{{R}'}}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}\Rightarrow \dfrac{1}{{{R}'}}=\dfrac{3}{R}\Rightarrow {R}'=\dfrac{R}{3}$. Hence, the net resistance of the circuit becomes one-third the value of the resistance in each branch.
Using the same formulation for N branches, we get: ${{R}_{net}}=\dfrac{R}{N}\to (1)$, where (R) is the resistance of each branch and (N) are the number of branches.
For the current problem, we have multiple $176\Omega $ in parallel to each other. These are connected to 220V line and the net current is 5A. Hence using the Ohm’s law and the value of resistance from equation (1), we get: $V=I{{R}_{net}}\Rightarrow 220=5\left( \dfrac{176}{N} \right)\Rightarrow N=\left( \dfrac{176}{44} \right)\Rightarrow N=4$.
Hence, 4 of the $176\Omega $ resistors in parallel would be required to get a net current of 5A flowing through a 220V line.
Note: It’s important to remember that in a parallel resistance circuit connection, the voltage drawn by all the resistances are equal. An everyday example of this is the way electricity reaches all our houses. The constant 220V voltage is supplied to all the households in a locality, since all the houses are in a parallel connection to each other.
Complete step by step solution:
Let’s find out how a parallel resistance circuit works. A parallel resistance circuit is made below.

The voltage source is (V) and the net amount of current flowing through the circuit is (I). There are three resistances: \[\left( {{R}_{1}} \right)\], \[\left( {{R}_{2}} \right)\] and \[\left( {{R}_{3}} \right)\]connected in parallel to each other. The amount of current through each branch of resistor is given by: \[\left( {{I}_{1}} \right)\], \[\left( {{I}_{2}} \right)\] and \[\left( {{I}_{3}} \right)\].
The values of the individual amount of current through each resistance, can be found through the Ohm’s law: $V=IR\Rightarrow I=\dfrac{V}{R}$. Hence, the value \[\left( {{I}_{1}} \right)\]is: \[{{I}_{1}}=\dfrac{V}{{{R}_{1}}}\]. Similarly, the value of \[\left( {{I}_{2}} \right)\]is: \[{{I}_{2}}=\dfrac{V}{{{R}_{2}}}\] and the value of \[\left( {{I}_{3}} \right)\]is: \[{{I}_{3}}=\dfrac{V}{{{R}_{3}}}\]. Using the Kirchoff’s current law: $I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}$.
Hence, $I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}$ becomes: $I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}\Rightarrow \dfrac{V}{R}=\dfrac{V}{{{R}_{1}}}+\dfrac{V}{{{R}_{2}}}+\dfrac{V}{{{R}_{3}}}\Rightarrow \dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$.
Let’s consider a special case of the resistances connected in parallel. In this case, the resistances are of same value, that is: $\dfrac{1}{{{R}'}}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}\Rightarrow \dfrac{1}{{{R}'}}=\dfrac{3}{R}\Rightarrow {R}'=\dfrac{R}{3}$. Hence, the net resistance of the circuit becomes one-third the value of the resistance in each branch.
Using the same formulation for N branches, we get: ${{R}_{net}}=\dfrac{R}{N}\to (1)$, where (R) is the resistance of each branch and (N) are the number of branches.
For the current problem, we have multiple $176\Omega $ in parallel to each other. These are connected to 220V line and the net current is 5A. Hence using the Ohm’s law and the value of resistance from equation (1), we get: $V=I{{R}_{net}}\Rightarrow 220=5\left( \dfrac{176}{N} \right)\Rightarrow N=\left( \dfrac{176}{44} \right)\Rightarrow N=4$.
Hence, 4 of the $176\Omega $ resistors in parallel would be required to get a net current of 5A flowing through a 220V line.
Note: It’s important to remember that in a parallel resistance circuit connection, the voltage drawn by all the resistances are equal. An everyday example of this is the way electricity reaches all our houses. The constant 220V voltage is supplied to all the households in a locality, since all the houses are in a parallel connection to each other.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Differentiate between action potential and resting class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




