Mesh Analysis

The electrical circuits are closed loops or paths that create a web of electrical parts through which electrons can move. Simple circuits can be investigated in circuit analysis utilising fundamental techniques like Ohm's law, KVL, and KCL. However, these techniques, along with series and parallel methods, are unreliable for a complicated circuit made up of numerous regulated sources. Therefore, nodal and mesh (or loop) analysis methods are utilised to determine the variables of a branch in such a circuit. Circuit variables like voltage and currents are easily determined in any branch without any effort utilising these traditional methods. Let's examine mesh analysis in more detail.

Mesh and Nodal Analysis

The process used to calculate the current flowing through a planar circuit is called mesh analysis. A planar circuit is characterised as a circuit drawn on a plane surface without any wires crossing one another. Kirchhoff's voltage law is applied in mesh analysis, which determines the currents in each loop. Kirchhoff's current law is applied in nodal analysis, which determines the voltages at each node in an equation.

Supermesh Analysis

When two meshes share a component as a source of current, super mesh analysis is used to solve large, complex circuits.

Mesh Analysis Steps

The following steps are to be followed:

• To recognize the meshes and to categorise the mesh currents as moving either clockwise or counterclockwise in loops.

• To measure the amount of mesh current that passes through each component.

• Kirchhoff's voltage law and then Ohm's law are used to write the mesh equations for all meshes.

• By continuing to Step 3, where the mesh equations are solved, the mesh currents are obtained.

• Consequently, using the node voltages, every electrical circuit current through any component and its voltage across any component can be calculated.

Mesh Current Analysis

Mesh Current Analysis is a method for determining the currents flowing around a loop or mesh inside of any circuit's closed path.

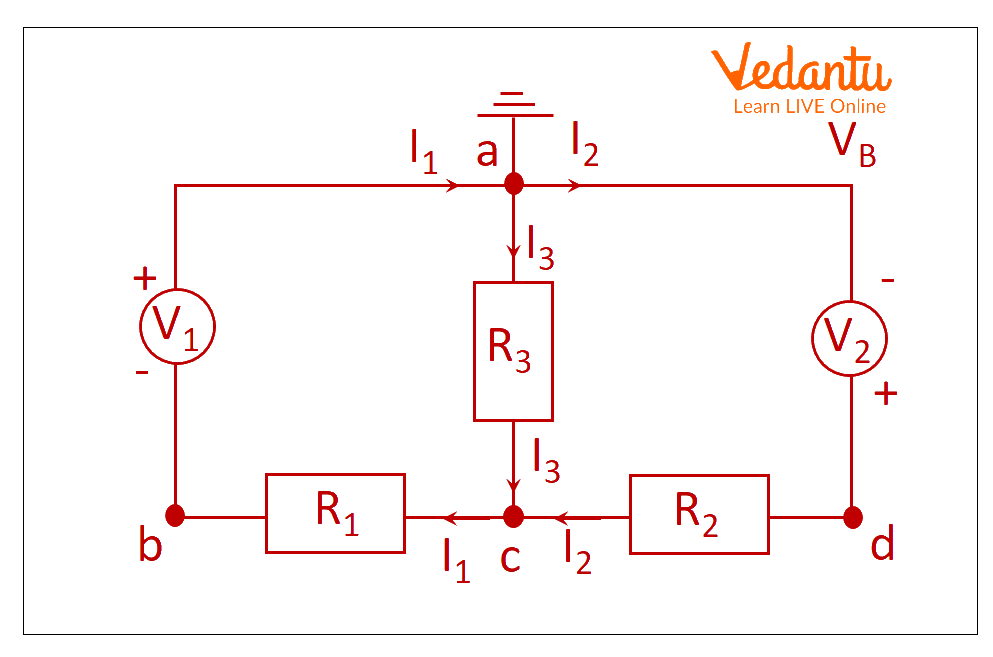
Closed Circuit Path

Mesh current analysis from closed circuit path.

Calculating the currents ${I_1}$ and I2 flowing in the two resistors using Kirchhoff's Current Law equations is a straightforward way to reduce the amount of Maths required. As I3 is simply the sum of I1 and I2 (According to Kirchoffs current law), there is no need to compute it.

Here, V1 = 10 V, V2 =20 V, R1 = 10 Ω, R2 = 20 Ω, and R3 = 40 Ω.

We know that V=R x I.

Thus, Kirchhoff's second voltage law is transformed into:

In the first loop, acba R3 is 40 and R1 and R3 are in series that becomes 50 Ohm.

\[10 = 10{I_1} + 40{I_3}\] (Equation No 1)

In the second loop adca, R3 is 40 and R2 and R3 are in series, which becomes 60 Ohm.

\[20 = 40{I_1} + 60{I_2}\] (Equation No 2)

Using this Mesh analysis formula, also known as Loop Analysis or Maxwell's Circulating Currents approach, is a simpler way to solve the circuit shown above. We must designate each "closed loop" acba and adca with a circulating current rather than just labelling the branch currents. Whenever there are Mesh analysis 3 loops, then Kirchhoff's Voltage Law (It says that the sum of voltages must be zero) is applied for every single loop among the three loops with currents I1, I2, and I3.

Interesting Facts of Mesh analysis

• Reduces the complexity of the circuit.

• Simplifies the calculations and reduces the mathematical equations to solve the circuit.

• Identifies the set of meshing equations by using KVL and KCL.

• It only applies to flat circuits.

Solved Problems

1. The battery value in the Mesh analysis examples circuit is 90 volts, the current source is 5 amps, and the three resistor values are 9 ohms, 6 ohms, and 8 ohms. Calculate the current through each resistor and the potential difference through each resistor using mesh analysis.

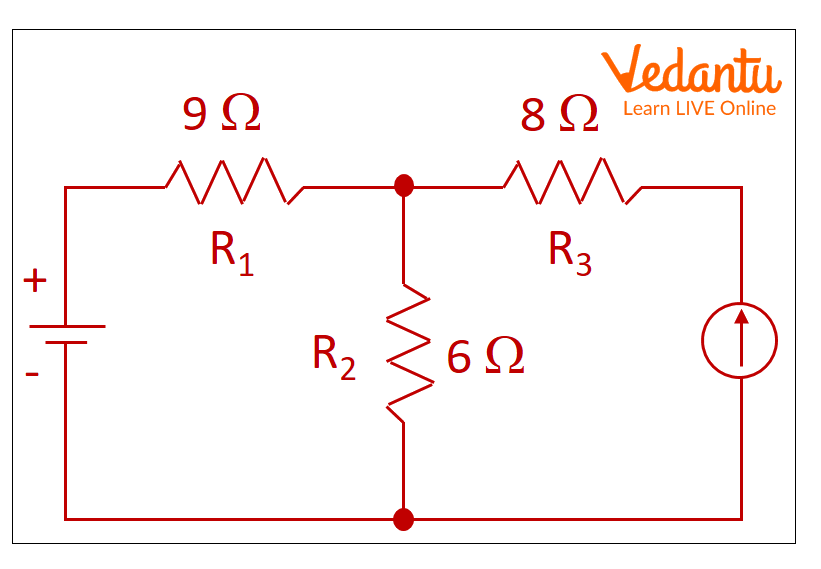
Example circuit

Solution:

At first, let’s define the ground as displayed in the figure.

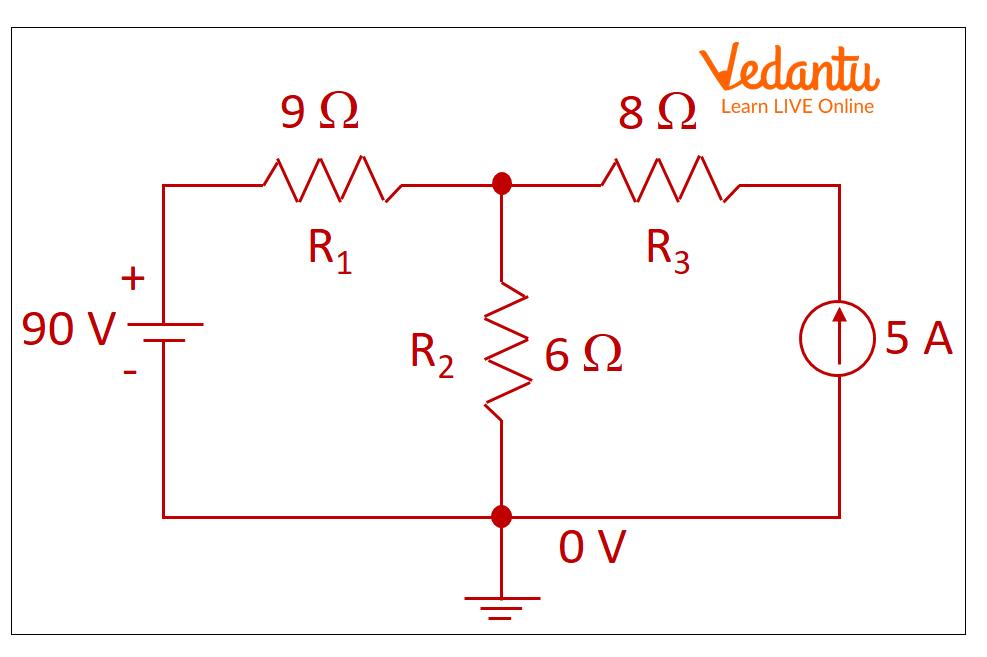
Example Circuit with Ground

Let VA, VB, and VC be the potential, as illustrated in the figure.

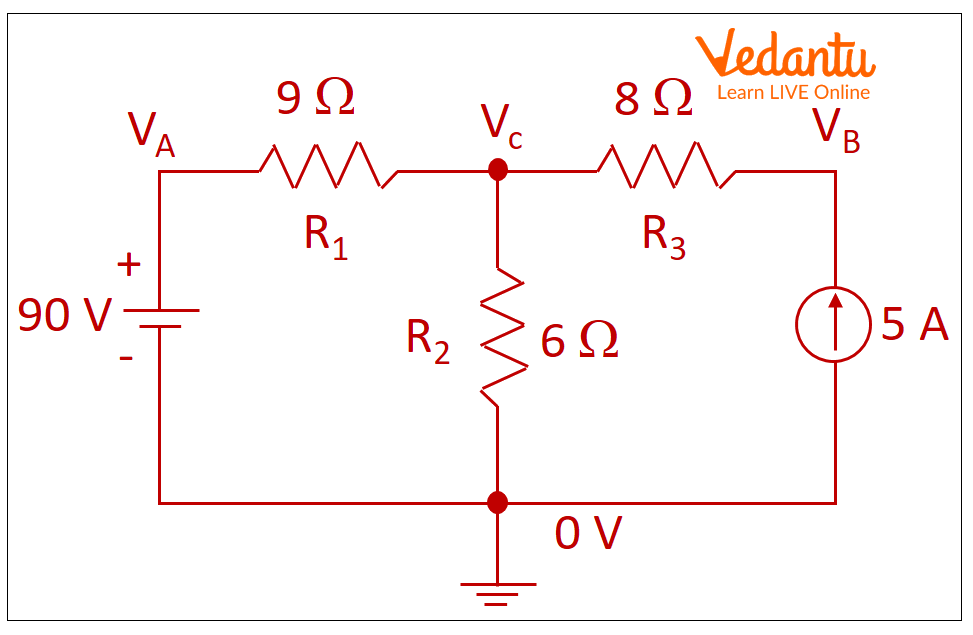
Example Circuit with Ground and Potential

As indicated in the picture, let I1 and I2 represent the currents running through the two loops in a clockwise direction.

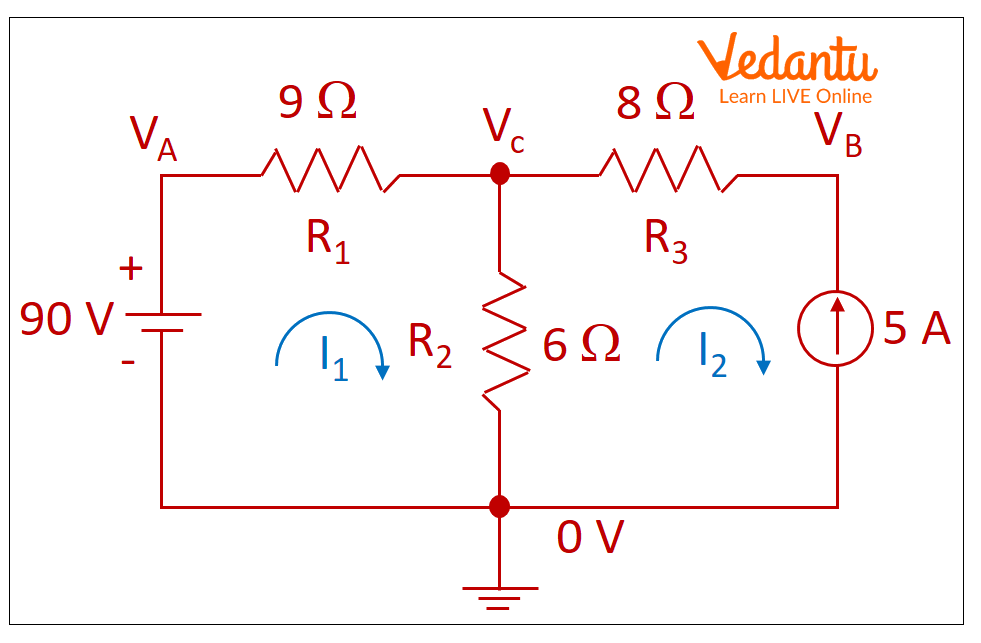
Example Circuit with Ground, Potential, and Current Loop

Consider VA, VB, and VC as the potential difference through the resistors R1, R2 and R3, respectively.

Thus,

\[0 = 90 - {I_1}{R_1} - {R_2}({I_1} - {I_2})\]

\[0 = 90 - 9{I_1} - 6({I_1} - {I_2})\]

\[ - 90 = - 15{I_1} + 6{I_2}\]

Dividing the equation with -3, we get

\[ - 30 = - 5{I_1} + 2{I_2}\]

The direction of actual current and I2 are opposite. So, putting I2 as -5, we have

\[{I_1} = 4Amp\]

Thus, 4 Amp current is flowing over R1 and 5 Amp current is flowing over R3.

The potential difference at VA is 90 V.

The potential difference at VB is given by VB = (I1 + I2) R2.

So, VB is 54 V.

The potential difference at VC is given by VC = I2 R3.

So, VC is 40 V.

2. Determine the current through a 10 Ohm resistor using the supermesh analysis in the given circuit.

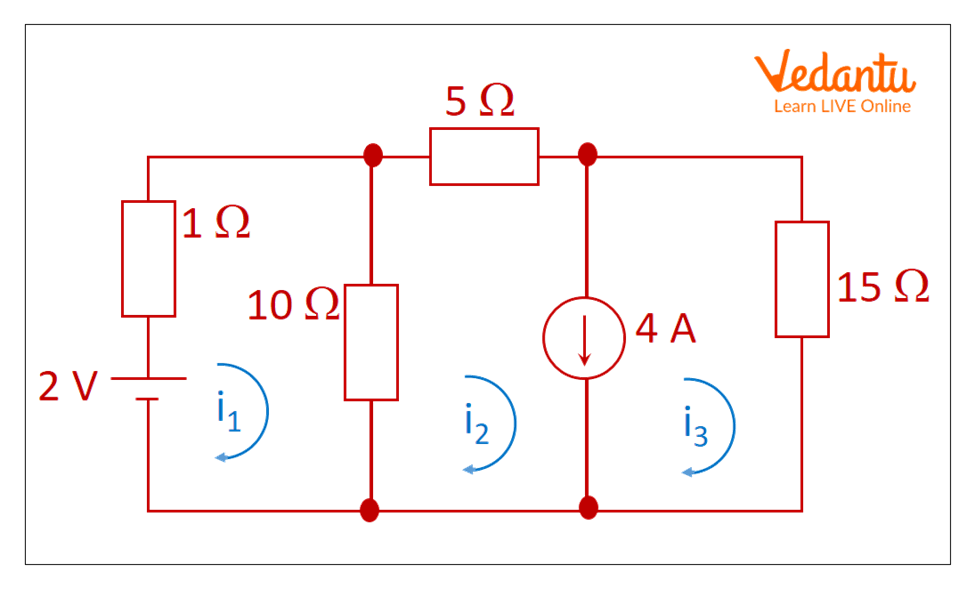
Example Circuit with Current Loops

Calculate the current through a 10 Ohm resistor using supermesh analysis.

Solution:

By application of KVL to mesh 1, we have

\[1{i_1} + 10({i_1} - {i_2}) = 2\]

\[11{i_1} - 10{i_2} = 2..........{\rm{(1)}}\]

Here, mesh 2 and 3 have 4A current source and as a result form a supermesh. The current from current source 4A is aligned with i3, so supermesh current is,

\[i = {i_2} - {i_3}\]

\[{i_2} - {i_3} = 4..........{\rm{(2)}}\]

By application of KVL to supermesh outer loop, we have

\[ - 10({i_2} - {i_1}) - 5{i_2} - 15{i_3} = 0\]

\[10{i_1} - 15{i_2} - 15{i_3} = 0..........(3)\]

Solution of equations 1, 2, and 3 give,

\[{i_1} = - 2.35{\rm{ A}}\]

\[{i_2} = - 2.78{\rm{ A}}\]

\[{i_3} = 1.22{\rm{ A}}\]

So, the current through 10 Ohm resistor given by,

\[{i_1} - {i_2} = - 2.35 + 2.78\]

\[{i_1} - {i_2} = 0.43{\rm{ A}}\]

Summary

Nodal and mesh (or loop) analysis methods can be utilised to determine the variables of a branch in such a circuit. Circuit variables like voltage and currents can be easily determined in any branch without any efforts and using these mesh and nodal analysis methods. When two meshes share a component as a source of current, super mesh analysis is used to solve large, complex circuits.