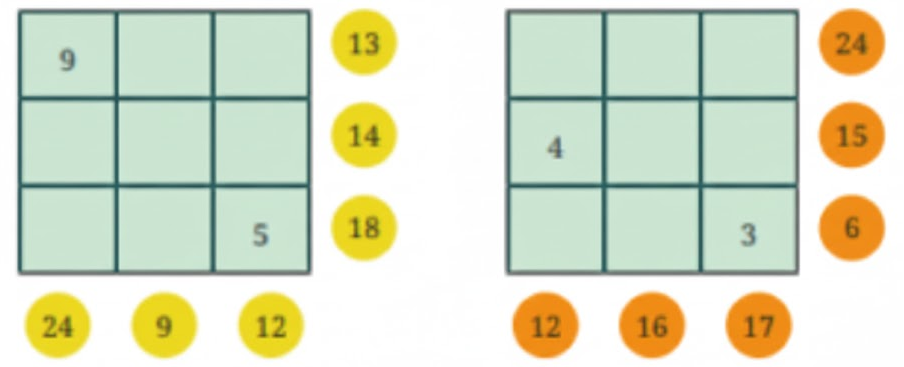
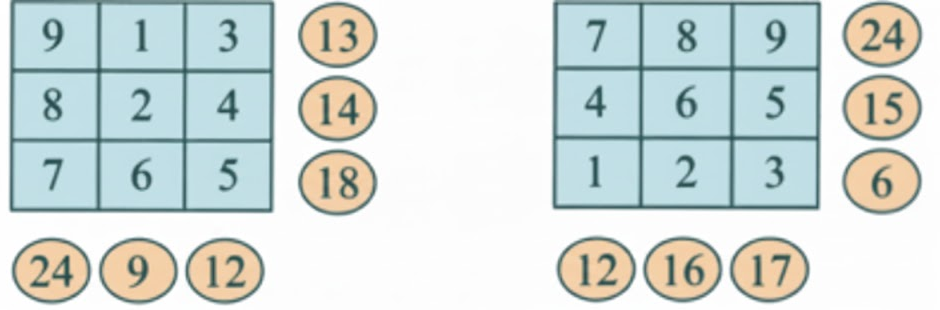
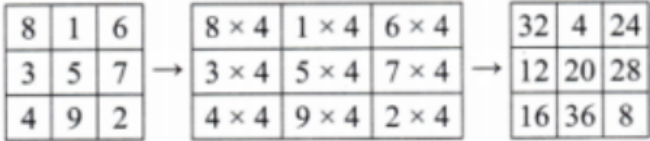
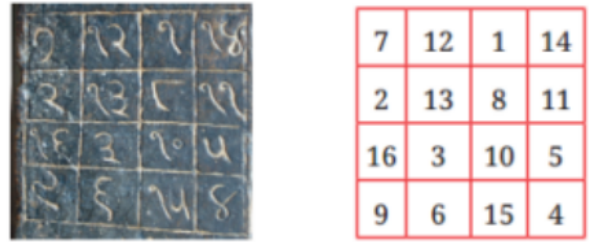
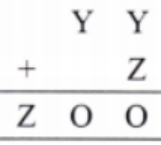
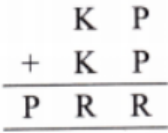
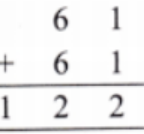
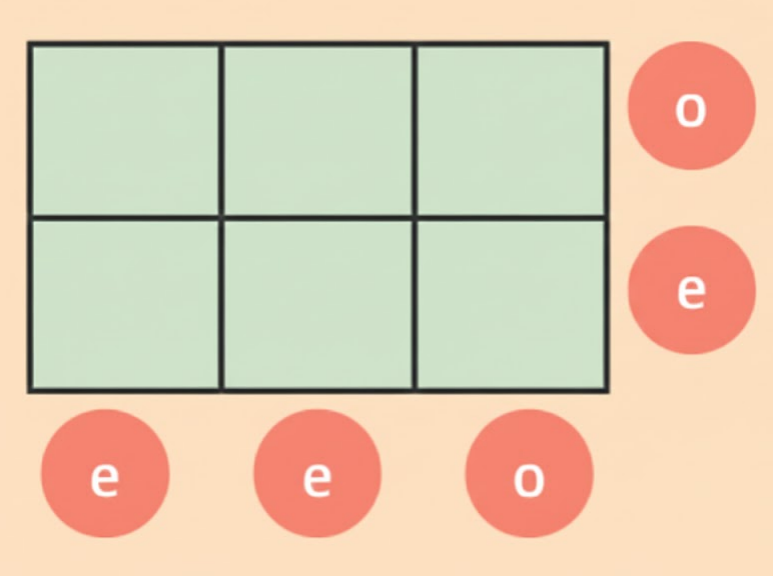
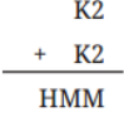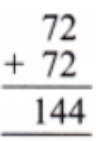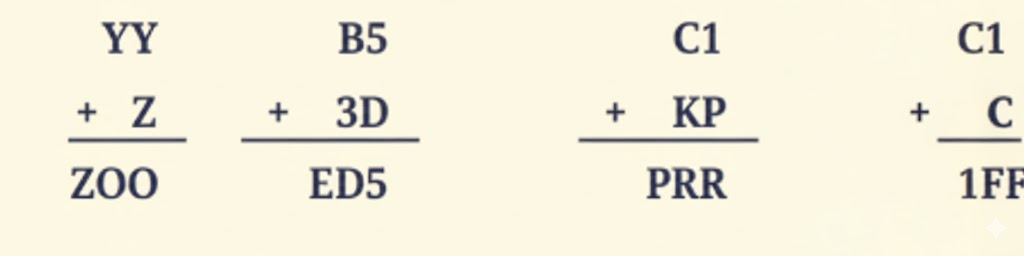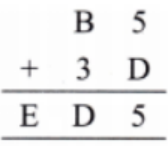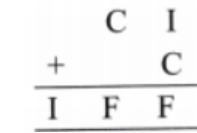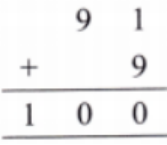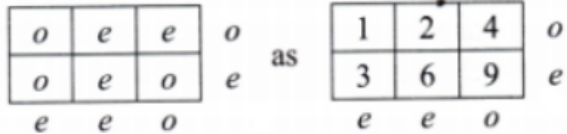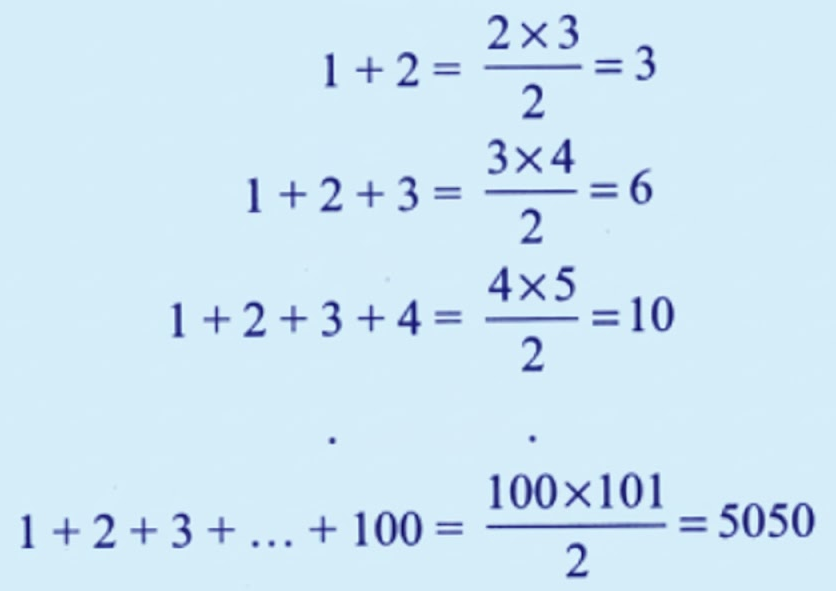How to Write Stepwise Answers for Number Play in Class 7 Maths
FAQs on NCERT Solutions For Class 7 Maths Chapter 6 Number Play (2025-26)
1. What are NCERT Solutions for Class 7 Maths Chapter 6 Number Play?
NCERT Solutions for Class 7 Maths Chapter 6 Number Play are step-by-step answers to all textbook and back exercise questions, designed according to the latest CBSE syllabus for 2025–26. These solutions help students learn concepts like factors, multiples, prime numbers, composite numbers, and tests of divisibility.
Key features include:
- Complete, accurate explanations for every exercise
- Use of diagrams, definitions, and important formulae
- Solutions formatted as per CBSE marking scheme
- Available in free PDF for offline study
2. How to write stepwise NCERT answers to score full marks in Class 7 Maths Chapter 6?
To score full marks, write stepwise NCERT answers using clear logic and CBSE-recommended structure.
Follow these tips:
- Start with a defined formula or rule (e.g., divisibility tests, factorization)
- Show all calculation steps, not just the final answer
- Use proper mathematical notation and symbols
- If asked, include neat diagrams or tables
- Highlight definitions, important results in your answers
3. Which questions from Chapter 6 Number Play are most likely to be asked in school exams?
Questions focusing on tests of divisibility, identification of prime and composite numbers, and stepwise problem-solving are often asked in exams.
Frequently tested topics include:
- Applying divisibility rules (2, 3, 4, 5, 9, 10, 11 etc.)
- Finding factors and multiples of given numbers
- Identifying if a number is prime or composite
- Short and long answer types explaining steps
4. Are diagrams or definitions compulsory in NCERT Solutions for Class 7 Maths Chapter 6?
Definitions are essential when asked in the question or needed to justify steps. Diagrams are not always compulsory in this chapter but can make answers clearer, especially for factor trees or explaining number concepts.
For best marks, always:
- Include definitions of key terms if relevant
- Draw factor trees/number line diagrams, if asked
5. How should I structure long answers in Number Play Chapter 6 for better marks?
Long answers should be structured logically, with clear steps and relevant explanations.
Tips for structuring:
- Start with the given data and what is to be found
- Write down relevant definitions/formulae
- Show each step of calculation with reasons (e.g., which divisibility rule you used)
- Conclude with a final answer statement
6. Where can I download a free PDF of NCERT Solutions for Class 7 Maths Chapter 6 Number Play?
You can download a free PDF of solutions for Class 7 Maths Chapter 6 Number Play from trusted educational websites that provide CBSE-aligned resources.
Advantages of downloading:
- Access offline study material anytime
- Easy revision and practice before exams
- Stepwise, teacher-verified answers included
7. What are the most important definitions and formulae to remember in Number Play Chapter 6?
Key definitions and formulae in Chapter 6 include:
- Factor: A number that divides another number without leaving a remainder
- Multiple: A number obtained by multiplying another number by an integer
- Prime Number: Has exactly two distinct factors: 1 and itself
- Composite Number: Has more than two factors
- Divisibility Rules: Rules to check if a number is divisible by 2, 3, 4, 5, 6, 9, 10, 11, etc.
8. How do I avoid common mistakes while answering Class 7 Maths Chapter 6 Number Play questions?
To avoid mistakes in Chapter 6 Number Play, pay attention to:
Do:
- Read questions thoroughly
- Apply correct divisibility rules
- Show all calculation steps
- Use proper definitions
- Skip steps or write only the final answer
- Mix up prime and composite number criteria
- Forget to provide reasons for true/false answers
9. Are NCERT Solutions for Class 7 Maths Chapter 6 Number Play sufficient for CBSE exams?
NCERT Solutions for Class 7 Maths Chapter 6 Number Play are sufficient for board and school exams, as they follow the latest CBSE syllabus and marking scheme.
For exam success:
- Practice all intext, back exercises, and exemplars
- Write answers stepwise as shown in solutions
- Revise key definitions and divisibility rules regularly
10. How can I revise Chapter 6 Number Play effectively in 1 day before exams?
To revise Chapter 6 Number Play in 1 day:
- Go through summary notes and formulae table
- Quickly solve one problem from each exercise
- Review divisibility rules and prime/composite examples
- Attempt 2–3 short and long questions for practice