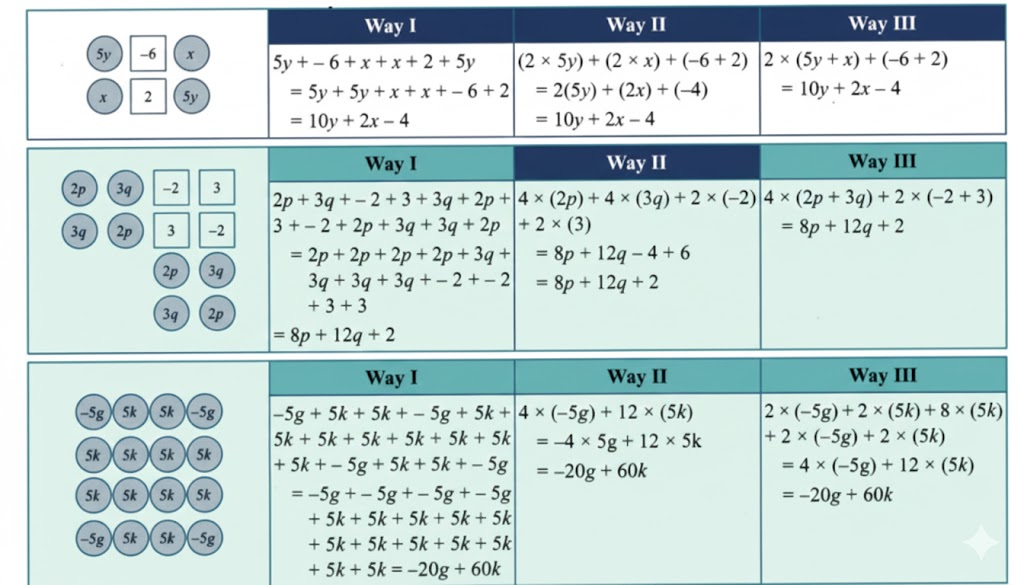
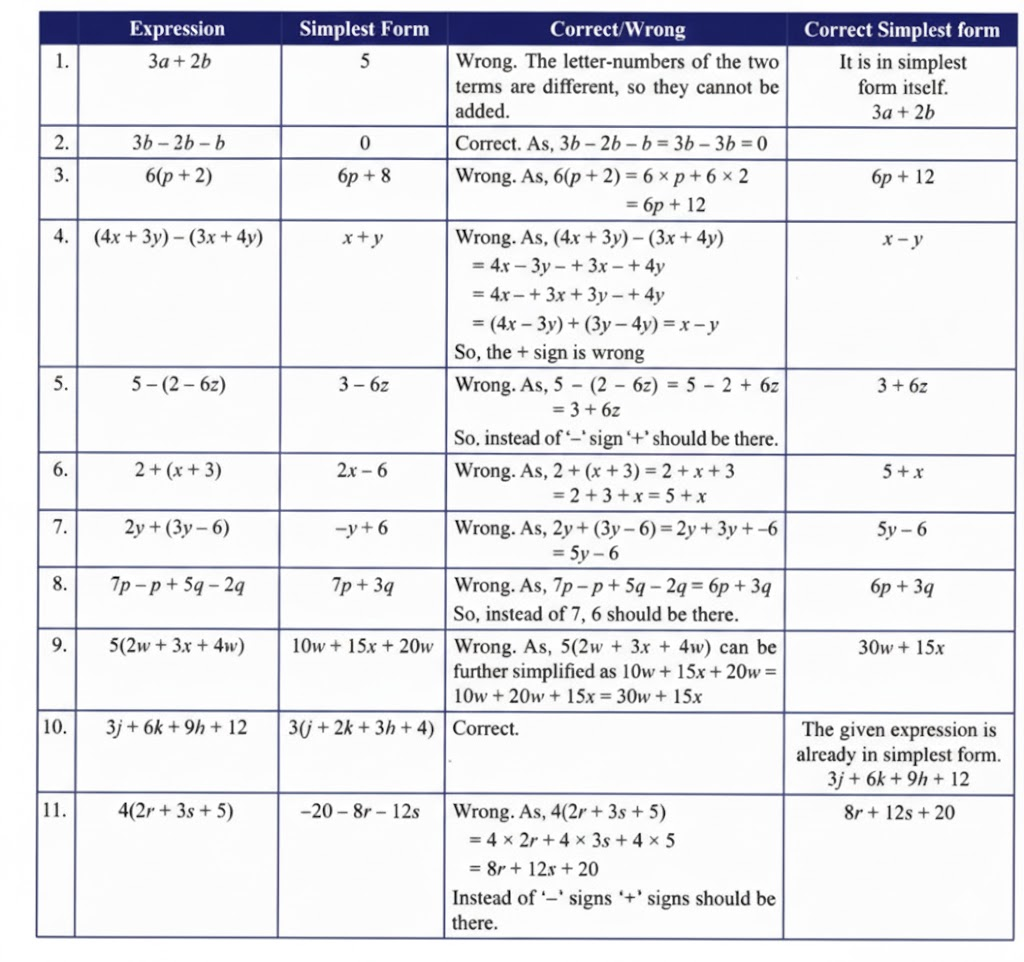
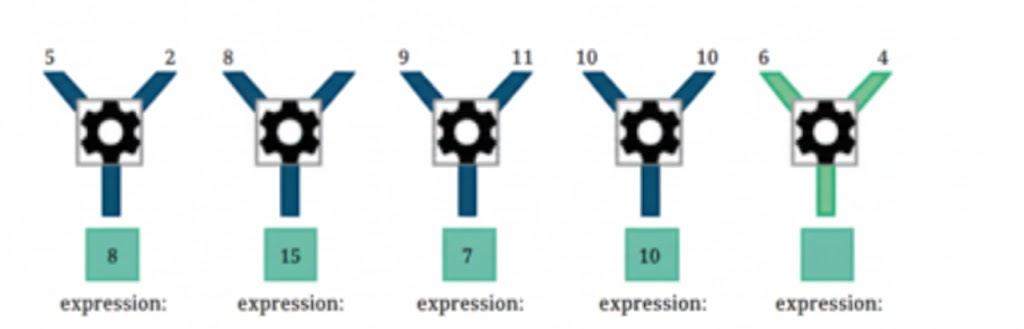
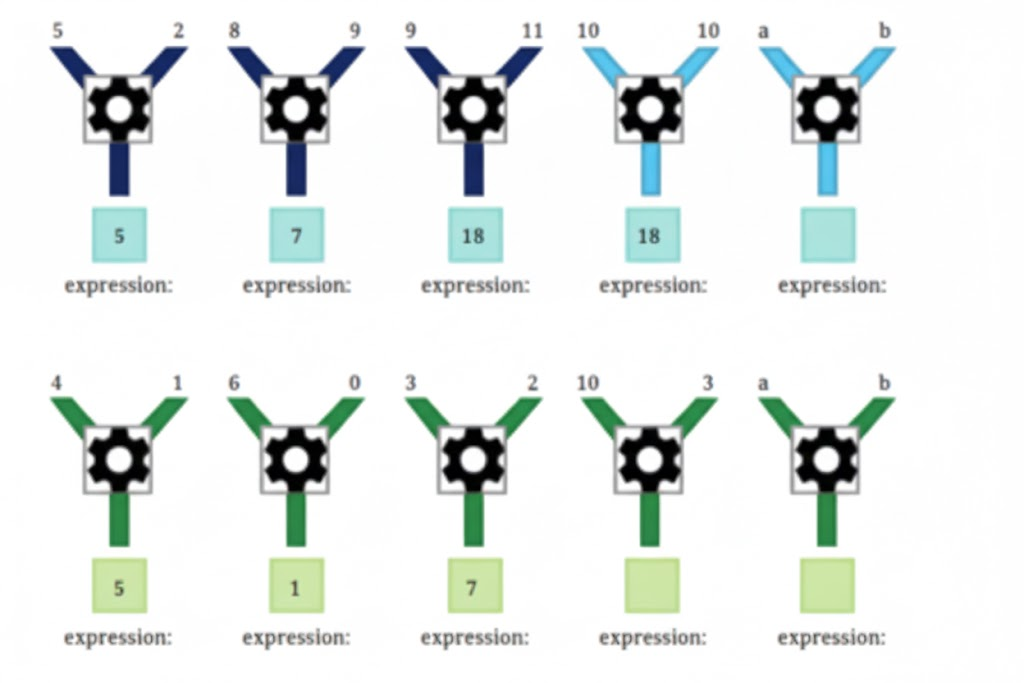
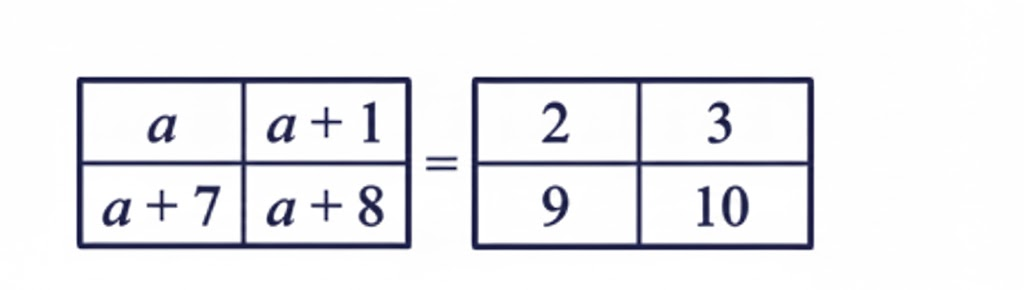
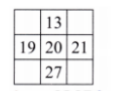
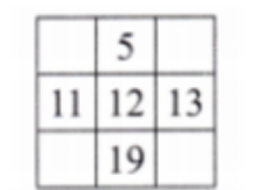
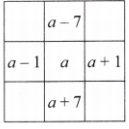
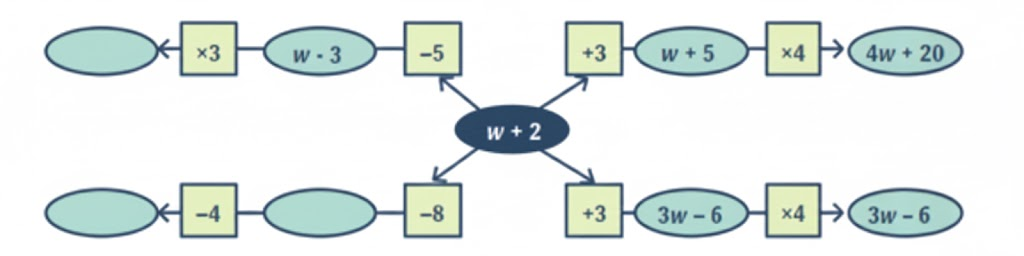
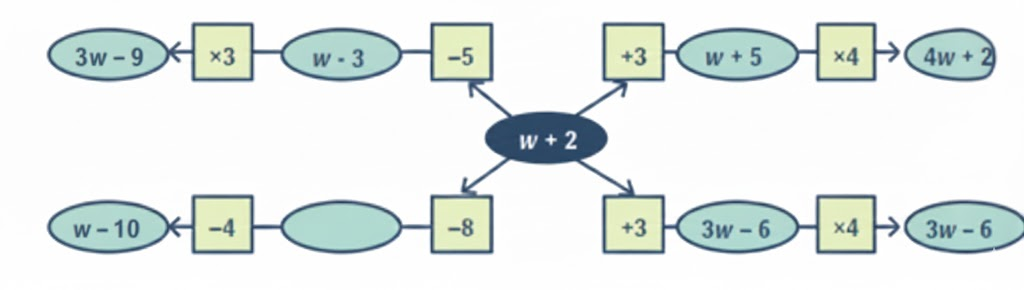
Exercise-wise Answers for Expressions using Letter-Numbers Class 7 Maths
FAQs on NCERT Solutions For Class 7 Maths Chapter 4 Expressions (2025-26)
1. What are NCERT Solutions for Class 7 Maths Chapter 4 Expressions using Letter-Numbers?
NCERT Solutions for Class 7 Maths Chapter 4 Expressions using Letter-Numbers offer stepwise answers to all textbook exercises, helping students master key concepts.
Highlights:
- Based on the latest CBSE 2025–26 syllabus
- Includes solved exercises and back questions
- Helps build exam confidence and clarity
- Available with free PDF download for offline study
2. How should I write stepwise NCERT answers for full marks in Class 7 Maths Chapter 4?
To score full marks in NCERT-based school exams, your answers for Chapter 4 should:
- Start with a clear statement of the given data
- Show every calculation step logically and sequentially
- Use correct mathematical notation and terms
- Highlight keywords like 'expression', 'variable', etc.
- Include a final answer box if required
3. Which topics from Expressions using Letter-Numbers are most important for exams?
The most important topics for exams in Chapter 4 are:
- Understanding and forming expressions using letters and numbers
- Using variables and distinguishing between constants and variables
- Writing expressions for word problems
- Applying rules of operations on algebraic expressions
- Solving intext and back exercises
4. Are diagrams or definitions compulsory in Class 7 Maths Chapter 4 exam answers?
Including definitions is advisable when questions ask for concept explanation.
Diagrams are not typically needed in this chapter, as it focuses on expressions, not geometry. However:
- Write precise definitions for terms like variable and constant as per NCERT
- Draw a simple box or highlight if asked to show the final form of an expression
5. Where can I download Class 7 Maths Chapter 4 NCERT Solutions PDF for free?
You can download the NCERT Solutions for Class 7 Maths Chapter 4 free PDF from trusted educational platforms.
Look for one-click PDF access and ensure the content is aligned with CBSE 2025–26.
6. How do I structure long answers in Class 7 Maths for better marks?
To structure long answers:
- Begin with a stepwise statement of what is given
- List formulae or rules used
- Show every calculation logically with clear steps
- Write the final result or conclusion in a separate line or box
- Use proper terminology as per the NCERT syllabus
7. What are key definitions and formulae needed for Class 7 Chapter 4 Expressions using Letter-Numbers?
Key definitions and formulae for Chapter 4 include:
- Variable: A letter that can take different values
- Constant: A value that does not change
- Expression: A combination of numbers, variables, and operations
- Algebraic expression: An expression with both numbers and letters
8. How can I revise Expressions using Letter-Numbers quickly before an exam?
Quick revision tips for Chapter 4 Expressions using Letter-Numbers:
- Review definitions and key formulae from your notes
- Practice exercise-wise NCERT solutions
- Try a 1-day, 3-day, or 7-day revision plan
- Attempt sample papers and MCQs for self-assessment
9. Do examiners award partial marks for correct steps even if the final answer is wrong in NCERT Maths?
Yes, in CBSE Class 7 Maths marking, partial marks are usually awarded for correct steps, even if the final answer is incorrect due to minor calculation mistakes.
- Show all calculation steps clearly
- Use labelled steps for each part
10. Are these NCERT solutions enough to score full marks in Class 7 Maths exams?
NCERT Solutions for Class 7 Maths Chapter 4 are usually sufficient for school exams if you:
- Practice all exercise and intext questions
- Revise key definitions, examples, and formulae
- Avoid common mistakes by careful stepwise work