NCERT Solutions for Class 7 Maths Chapter 11 - In Hindi

ावली 11 .1 

1: एक आयताकार भूखंड की लम्बाई और चौड़ाई क्रमशः \[\mathbf{500}\] mतथा \[\mathbf{300}\] m है। ज्ञात कीजिये:

1. भूखंड का क्षेत्रफल? 

2. भूखंड का मूल्य, यदि \[\mathbf{1}\] $m^2$का मूल्य रुपये \[\mathbf{10}, \mathbf{000}\] है। 

उत्तर:

दिया है: आयताकार भूखंड की लम्बाई = \[\text{5}00\] mऔर 

आयताकार भूखंड की चौड़ाई= \[\text{3}00\] m

1. आयताकार भूखंड का क्षेत्रफल=लम्बाई x चौड़ाई 

= \[\text{5}00\] m× \[\text{3}00\] m

= \[\text{1}, \text{5}0, 000\] $m^2$

2. 1$m^2$भूखंड का मूल्य= रुपये \[\text{1}0, 000\] 

उत्तर: इसलिए \[\text{1}, \text{5}0, 000\] $m^2$भूखंड का मूल्य = \[\text{1}, \text{5}0, 000\times \text{1}0, 000\] = \[\text{1}, \text{5}0, 00, 00, 000\] $m^2$

2: एक वर्गाकारपार्क का क्षेत्रफल ज्ञात कीजिये जिसका परिमाप \[\mathbf{320}\] mहै।

उत्तर:

दिया है: वर्गाकार पार्क का परिमाप = \[\mathbf{320}\] m

 \[\text{4}\] × भुजा = \[\mathbf{320}\] 

भुजा = \[\frac{360}{4}\] = \[\text{8}0\] m 

अब वर्गाकार पार्क का क्षेत्रफल =भुजा× भुजा = \[\text{8}0\times \text{8}0\text{ }=\text{64}00\] $m^2$

अतः वर्गाकार पार्क का क्षेत्रफल \[\text{64}00\] $m^2$है।

3: एक आयताकार भूखंड की चौड़ाई ज्ञात कीजिये यदि इसका क्षेत्रफल \[\mathbf{440}\] $m^2$और लम्बाई \[\mathbf{22}\] mहो। इसका परिमाप भी ज्ञात कीजिये।

उत्तर:

दिया है: आयताकार भूखंड का क्षेत्रफल = \[\text{44}0\] $m^2$

लम्बाई× चौड़ाई = \[\text{44}0\] $m^2$

 \[\text{22}\] m ×चौड़ाई = \[\text{44}0\] $m^2$

चौड़ाई= \[\frac{440}{22}\] = \[\text{2}0\] m

इसलिए आयताकार भूखंड का परिमाप = \[\text{2}\] × (लम्बाई× चौड़ाई)

\[=\text{2}\times \text{ }(\text{22}+\text{2}0)\] 

\[=\text{2}\times \text{42 }=\text{84}\] m 

अतः आयताकार भूखंड का परिमाप \[\text{84}\] mहै।

4: एक आयताकार शीट का परिमाप \[\mathbf{100}\] cm है। यदि लम्बाई \[\mathbf{35}\] cm हो तो इसकी चौड़ाई ज्ञात कीजिए। क्षेत्रफल भी ज्ञात कीजिये?

उत्तर:

दिया है: आयताकार शीट का परिमाप = \[\text{1}00\] cm 

\[\text{2}\] × (लम्बाई+ चौड़ाई) = \[\text{1}00\] cm

\[\text{2}\] × ( \[\text{35}\] + चौड़ाई) = \[\text{1}00\] cm

 \[\text{35}\] + चौड़ाई = \[\frac{100}{2}\] 

 \[\text{35}\] + चौड़ाई= \[\text{5}0\] 

चौड़ाई= \[\text{5}0-\text{35}\] = \[\text{15}\] cm

इसलिए आयताकार शीट का परिमाप=(लम्बाई × चौड़ाई)

= \[(\text{35}\times \text{15})\text{ }=\text{525}\] 𝑐$m^2$

अतः आयातकार शीट तथा क्षेत्रफल क्रमशः \[\text{15}\] cmऔर \[\text{525}\] 𝑐$m^2$ है।

5: एक वर्गाकारपार्क का क्षेत्रफल आयताकार पार्क के बराबर है। यदि एक वर्गाकारपार्क की \[\mathbf{60}\] mहो और आयताकार पार्क की लम्बाई \[\mathbf{90}\] m हो तोआयताकार पार्क की चौड़ाई ज्ञात कीजिये।

उत्तर:

दिया है: वर्गाकार पार्क की भुजा= \[\text{6}0\] m

आयताकार पार्क की लम्बाई = \[\text{9}0\] m

के अनुसार, 

वर्गाकार पार्क का क्षेत्रफल =आयताकार पार्क का क्षेत्रफल

भुजा× भुजा = लम्बाई × चौड़ाई

 \[\text{6}0\times \text{6}0\text{ }=\text{ 9}0\times \] चौड़ाई

चौड़ाई = \[\frac{60\times \text{6}0}{90}\] = \[40\] m

अतः आयताकार पार्क की चौड़ाई \[40\] m है।

6: एक तार आयत के आकार का है। इसकी लम्बाई \[\mathbf{40}\] cm और चौड़ाई \[\mathbf{22}\] cm है। यदि उसी तार को दोबारा मोड़ कर एक वर्ग बनाया जाता है तो प्रत्येकभुजा की माप क्या होगी ?यह भी ज्ञात कीजिये की किस आकार का क्षेत्रफल अधिक होगा।

उत्तर:के अनुसार, 

वर्ग का परिमाप = आयत का परिमाप

 \[\text{4}\] × भुजा = \[\text{2}\] (लम्बाई+ चौड़ाई)

\[\text{4}\] × भुजा= \[\text{2 }\left( \text{4}0+\text{ 22} \right)\] 

 \[\text{4}\] × भुजा = \[\text{2}\times \text{ }(\text{62})\] 

भुजा = \[\frac{\text{2}\times \text{62}}{4}\] = \[\text{31}\] cm

7: एक आयत का परिमाप \[\mathbf{130}\] cm है। यदि आयात की चौड़ाई \[\mathbf{30}\] cm हो तोआयत की लम्बाई ज्ञात कीजिये। आयत का क्षेत्रफल भी ज्ञात कीजिये।

उत्तर:आयत का परिमाप = \[\mathbf{130}\] cm 

 \[2\] (लम्बाई+ चौड़ाई) = \[\mathbf{130}\] cm 

 \[2\] (लम्बाई+ \[\mathbf{30}\] ) = \[\mathbf{130}\] cm 

लम्बाई+ \[\mathbf{30}\] = \[\frac{130}{2}\] 

लम्बाई+ \[\text{3}0\] = \[\text{65}\] , लम्बाई= \[\text{65}-\text{3}0=\text{35}\] cm

आयत का क्षेत्रफल= लम्बाई x चौड़ाई = \[\text{35x3}0=\text{1}0\text{5}0\] 

अतः आयत का क्षेत्रफल \[\text{1}0\text{5}0\] 

8: \[\mathbf{2}\] mलम्बाई और \[\mathbf{1}\] mचौड़ाई वाले दरवाजे को एक दिवार में लगायाजाता है। दिवार की लम्बाई \[\mathbf{4}.\mathbf{5}\] तथा चौड़ाई \[\mathbf{3}.\mathbf{6}\] है। \[\mathbf{20}\] रुपए प्रति की दर सेदिवारपर सवेदीकराने का व्यय ज्ञात कीजिये।

उत्तर:आयताकार दरवाजे का क्षेत्रफल=लम्बाई xचौड़ाई

\[=\text{2x1}=\text{2}\] 

दरवाजे सहित दिवार का क्षेत्रफल=लम्बाई xचौड़ाई

 \[=\text{4}.\text{5x3}.\text{6}=\text{16}.\text{2}\] 

दरवाजे रहित दिवार का क्षेत्रफल=दरवाजे सहित दिवार का क्षेत्रफलदरवाजे का क्षेत्रफल

\[=\text{16}.\text{2}-\text{2}=\text{14}.\text{2}\] m2

1$m^2$ पर सफेदी करने का व्यय = ₹ \[\text{2}0\] 

इसलिए \[\text{14}.\text{2}\] दिवार पर सफेदी करने का व्यय= \[\text{2}0\text{x14}.\text{2 }=\text{284}\] 

अतः20₹ प्रति की दर से दिवार पर सफेदी करने का व्यय = ₹ \[\text{284}\] 

ावली 11. 2 

1:निम्न में से प्रत्येक समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिये।

(“Image will be updated soon”)

उत्तर:

(a) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{7x4}\] 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{28}\] 𝑐$m^2$

(b) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{5x3}\] 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{15}\] 𝑐$m^2$

(c) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{2}.\text{5x3}.\text{5}\] 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{8}.\text{75}\] 𝑐$m^2$

(d) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{5x4}.\text{8}\] 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{24}\] 𝑐$m^2$

(e) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{2x4}.\text{4}\] 

समान्तरचतुर्भुज का क्षेत्रफल= \[\text{8}.\text{8}\] 𝑐$m^2$

2:निम्न में प्रत्येक त्रिभुज का क्षेत्रफल ज्ञात कीजिये।

(“Image will be updated soon”)

उत्तर:

(a) त्रिभुज का क्षेत्रफल= \[\frac{1}{2}\] × (आधार × ऊँचाई) 

त्रिभुज का क्षेत्रफल = \[\frac{1}{2}\times (\text{4}\times \text{3})\] 

 \[=\text{ 6}\] 𝑐$m^2$

(b) त्रिभुज का क्षेत्रफल= \[\frac{1}{2}\] × (आधार × ऊँचाई) 

त्रिभुज का क्षेत्रफल = \[\frac{1}{2}\times (\text{5}\times \text{3}.\text{2})\] 

 \[=\text{ 8}\] 𝑐$m^2$

(c) त्रिभुज का क्षेत्रफल= \[\frac{1}{2}\] × (आधार × ऊँचाई) 

त्रिभुज का क्षेत्रफल = \[\frac{1}{2}\times (\text{3}\times \text{4})\]

\[=\text{ 6}\] 𝑐$m^2$

(d) त्रिभुज का क्षेत्रफल= \[\frac{1}{2}\] × (आधार × ऊँचाई) 

त्रिभुज का क्षेत्रफल = \[\frac{1}{2}\times (\text{3}\times \text{2})\] 

 \[=\text{ 3}\] 𝑐$m^2$

3: रिक्त स्थान का मान ज्ञात कीजिये।

(“Image will be updated soon”)

उत्तर:

(f) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

 \[\text{246 }=\text{ 2}0\text{x}\] ऊँचाई

ऊँचाई = \[\frac{246}{20}=12.3\] cm

(g) समान्तरचतुर्भुज का क्षेत्रफल = (आधार × ऊँचाई) 

 \[\text{154}.\text{5 }=\] आधार x \[\text{15}\] 

आधार = \[\frac{154.5}{15}=10.3\] cm

(h) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

 \[48.72=\] आधार x \[8.4\] 

आधार = \[\frac{48.72}{8.4}=5.8\] cm

(i) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

 \[\text{16}.\text{38 }=\text{ 15}.\text{6}\] x ऊँचाई

ऊँचाई = \[\frac{16.38}{15.6}=1.05\] cm

4: रिक्त स्थानों का मान ज्ञात कीजिये।

(“Image will be updated soon”)

उत्तर:

(e) त्रिभुज का क्षेत्रफल= \[\frac{1}{2}\] × (आधार × ऊँचाई) 

 \[\text{87 }=\text{ 15}\] x ऊँचाई

ऊँचाई = 

 \[\frac{87}{15}\] 𝑐𝑚 = \[\text{11}.\text{6}\] 𝑐𝑚

(f) त्रिभुज का क्षेत्रफल= \[\frac{1}{2}\] × (आधार × ऊँचाई) 

 \[\text{1256 }=\] आधार x \[\text{31}.\text{4}\] 

आधार = \[\frac{1256}{31.4}\] 𝑚𝑚 = \[80\] 𝑚𝑚

(g) त्रिभुज का क्षेत्रफल= \[\frac{1}{2}\] × (आधार × ऊँचाई) 

 \[\text{17}0.\text{5 }=\text{ 22}\] x ऊँचाई

ऊँचाई = \[\frac{170.5}{22}\] 𝑐𝑚 = \[15.5\] 𝑐𝑚

5:PQRS समान्तर चतुर्भुज है। (आकृति 11.23).QM शीर्षQ से SR तक की ऊँचाई तथा QN शीर्षQ से PS तक की ऊँचाई है। यदि SR= \[\mathbf{12}\] cmऔरQM= \[\mathbf{7}.\mathbf{6}\] cmतो ज्ञात कीजिये: 

(a)समान्तरचतुर्भुज PQRS का क्षेत्रफल (b)QN, यदिPS= \[\mathbf{8}\] cm

(“Image will be updated soon”)

उत्तर:

(a) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

\[=\text{ 12x7}.\text{6}\] 

 \[=\text{ 91}.\text{2}\] 𝑐$m^2$

(b) समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

\[\text{91}.\text{2 }=\text{ 8}\] x QN 

QN = \[\text{11}.\text{4}\] cm

6:DLऔर BM समान्तरचतुर्भुज ABCD की क्रमशः भुजाएँ AB औरAD परलंब है। (आकृति 11. 24) यदि समान्तर चतुर्भुज का क्षेत्रफल \[\mathbf{1470}\] है AB= \[\mathbf{35}\] cmऔर AD= \[\mathbf{49}\] cm है, तो BM तथा DLकी लम्बाई ज्ञात कीजिये।

(“Image will be updated soon”)

उत्तर:AB = \[\text{35}\] cm और AD= \[\text{49}\] cm 

समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

 \[\text{147}0\text{ }=\text{ 35}\] x DL 

DL = \[\frac{1470}{35}=42\] cm

समान्तरचतुर्भुज का क्षेत्रफल= (आधार × ऊँचाई) 

 \[\text{147}0\text{ }=\text{ 49}\] x BM 

DL = \[\frac{1470}{49}\] \[=\text{ 3}0\] cm

7: त्रिभुज ABC, A पर समकोण है (आकृति 11.25) और AD भुजा पर लंब है। यदि AB= \[\mathbf{5}\] cm, BC= \[\mathbf{13}\] cm और AC= \[\mathbf{12}\] cm है, तो ΔABCका क्षेत्रफल ज्ञात कीजिये। AD की लम्बाई भी ज्ञात कीजिये।

(“Image will be updated soon”)

उत्तर:ΔABC में AB = \[\text{5}\] cm और AC= \[\text{12}\] cm 

त्रिभुज का क्षेत्रफल= \[\frac{1}{2}\] × (आधार × ऊँचाई) 

= \[\frac{1}{2}\] x (AB x AC) 

= \[\frac{1}{2}\text{x5x12}=\text{3}0\] 𝑐$m^2$

त्रिभुज ABC का क्षेत्रफल = \[\frac{1}{2}\] x (BC x AD) 

 \[30=\frac{1}{2}\] x \[\text{13}\] x AD 

 AD = \[\frac{60}{13}\] cm

8:ΔABC समद्विबाहु त्रिभुज है जिसमे AB=AC= \[\mathbf{7}.\mathbf{5}\] cm और BC= \[\mathbf{9}\] cm है। (आकृति 11.26) A से BC तक की ऊँचाई AD, \[\mathbf{6}\] cm है। ΔABC का क्षेत्रफल ज्ञात कीजिये C से AB तक की ऊँचाई, अर्थात CE क्या होगी ?

(“Image will be updated soon”)

उत्तर:

ΔABC में AD = \[\text{6}\] cm और BC= \[\text{9}\] cm 

त्रिभुज का क्षेत्रफल= \[\frac{1}{2}\] × (आधार × ऊँचाई) 

= \[\frac{1}{2}\] x (BC \times AD) 

= \[\frac{1}{2}\text{x9x6}=\text{27}\] 𝑐$m^2$

त्रिभुज ABC का क्षेत्रफल == \[\frac{1}{2}\] x (AB x CE) 

 \[27=\frac{1}{2}\] x \[\text{7}.\text{5}\] x CE 

 CE = \[\text{7}.\text{2}\] cm 

अतः C से AB तक की ऊँचाई अर्थात CE की लम्बाई \[\text{7}.\text{2}\] cm हैं।

ावली 11.3 

1: निम्न त्रिज्याओं वाले व्रतोंकी परिधि ज्ञात कीजिए : (𝜋 = \[\frac{22}{7}\] लीजिए) 

(a) \[\mathbf{14}\] cm 

(b) \[\mathbf{28}\] cm 

(c) \[\mathbf{21}\] cm

उत्तर:

(a) वृत की परिधि = \[\text{2}\] 𝜋𝑟 \[=\text{2}\times \frac{22}{7}\times \text{14 }=\text{ 88}\] cm 

(b) वृत की परिधि = \[\text{2}\] 𝜋𝑟 = \[\text{2}\] cm 

(c) वृत की परिधि = 2𝜋𝑟 = \[=\text{2}\times \frac{22}{7}\times 21=\text{ 132}\] cm 

2: निम्न व्रतोंका क्षेत्रफल ज्ञात कीजिए। दिया गया है : (𝜋 = \[\frac{22}{7}\] लीजिए)

(a) त्रिज्या = \[\mathbf{14}\] mm 

(b) व्यास = \[\mathbf{49}\] m

(c) त्रिज्या = \[\mathbf{5}\] cm

उत्तर:

(a) वृत का क्षेत्रफल = $𝜋𝑟^2$= 

 \[\frac{22}{7}\times \text{14}\times \text{14 }=\text{ 22}\times \text{2}\times \text{14 }=\text{ 616}\] m$m^2$

(b) व्यास = \[\text{49}\] m

∴ त्रिज्या = \[\frac{49}{2}=24.5\] m

∴ वृत का क्षेत्रफल = $𝜋𝑟^2$

= \[\frac{22}{7}\times \text{24}.\text{5}\times \text{24}.\text{5}=\text{ 22}\times \text{3}.\text{5}\times \text{24}.\text{5 }=\text{ 1886}.\text{5}\] $m^2$

(c) वृत का क्षेत्रफल = $𝜋𝑟^2$= \[\frac{22}{7}\times \text{5}\times \text{5 }=\frac{550}{7}=\text{ 78}.\text{5}\] $cm^2$

3: यदि एक वृत्ताकार शीट की परिधि \[\mathbf{154}\] mहो तो इसकी त्रिज्याज्ञात कीजिए। शीट का क्षेत्रफल भी ज्ञात कीजिए।(𝜋 = \[\frac{22}{7}\] लीजिए)

उत्तर:

वृत्ताकार की परिधि= \[\text{154}\] m

→ \[\text{2}\] 𝜋𝑟 = \[\text{154}\] m

→r = \[\frac{154}{\text{2}\pi }=\frac{\text{154}\times \text{7}}{\text{2}\times \text{22}}=24.5\] m

इसलिए, वृत्ताकार शीट का क्षेत्रफल = $𝜋𝑟^2$ = \[\frac{22}{7}\times \text{24}.\text{5}\times \text{24}.\text{5 }=\text{1886}.\text{5}\] $m^2$

अतः वृत्ताकार शीट की त्रिज्या तथा क्षेत्रफल क्रमशः \[\text{24}.\text{5}\] mऔर

 \[\text{1886}.\text{5}\] $m^2$है। 

4: \[\mathbf{21}\] mव्यास वालेके वृत्ताकार बगीचेके और माली बाड़ चाहता है। ख़रीदे जाने वाले वालेआवश्यक रस्सेकी लम्बाई ज्ञातकीजिए, यदि वह \[\mathbf{2}\] पूरे चक्कर की बनाना चाहता है। ₹ \[\mathbf{4}\] प्रतिमीटर कीदर सेरस्सेपर व्यय ज्ञात कीजिए।

उत्तर:

वृत्ताकार बगीचे का व्यास = \[\text{21}\] m

∴ वृत्ताकार बगीचे की त्रिज्या = \[\frac{21}{2}\] m

इसलिए, वृत्ताकार बगीचे की परिधि = \[\text{2}\] 𝜋𝑟 \[=\text{ 2}\times \frac{22}{7}\times \frac{21}{2}=\text{ 22}\times \text{3}=\text{ 66}\] m

 \[\text{2}\] पुरे चक्कर की बाड़ बनाने के लिए आवश्यक रस्से की लम्बाई = 

 \[\text{2}\times \text{2}\] 𝜋𝑟

 \[=\text{ 2}\times \text{66}=\text{ 132}\] m 

 \[\text{1}\] मीटर रस्से पर व्यय = ₹ \[\text{4}\] 

इसलिए, 132 मीटर रस्से पर व्यय \[=\text{ 4}\times \text{132 }=\] ₹ \[\text{528}\]

5: \[\mathbf{4}\] cm त्रिज्या वाली एक वृत्ताकार शीट में से \[\mathbf{3}\] cm त्रिज्या वालीएक वृत क निकाल दिया जाता है। शीट के शेष भाग का क्षेत्रफल ज्ञातकीजिए। (𝜋 = \[\mathbf{3}.\mathbf{14}\] लीजिए)

उत्तर:

वृत्ताकार शीट की व्यास (R) = \[\text{4}\] cm 

निकाले गए वृत्त की त्रिज्या (r) = \[\text{3}\] cm 

शीट के शेष भाग का क्षेत्रफल=वृत्ताकार शीट का क्षेत्रफल निकाले गएवृत्त का क्षेत्रफल 

= $𝜋𝑅^2$ − $𝜋𝑟^2$= 𝜋($𝑅^2$ − $𝑟^2$)

= 𝜋 \[\left( {{\text{4}}^{\text{2}}}-\text{ }{{\text{3}}^{\text{2}}} \right)\] = 𝜋 \[\left( \text{16 }-\text{ 9} \right)\] 

 \[=\text{ 3}.\text{14}\times \text{7 }=\text{ 21}.\text{98}\] $cm^2$

अतः, शीट के शेष भाग का क्षेत्रफल \[\text{21}.\text{98}\] $cm^2$है। 

6: साइमा \[\mathbf{1}.\mathbf{5}\] mव्यास वालेएक वृत्ताकार टेबल कवर के चारोंऔरकिनारीलगाना चाहती है। आवश्यककिनारी की लम्बाई ज्ञात कीजिएऔर ₹ \[\mathbf{15}\] प्रतिमीटर की दर से किनारी का व्यय ज्ञात कीजिए।(𝜋 = \[\mathbf{3}.\mathbf{14}\] लीजिए)

उत्तर:

वृत्ताकार टेबल कवर का व्यास = \[\text{1}.\text{5}\] m

∴ वृत्ताकार टेबल कवर की त्रिज्या = \[\frac{1.5}{2}\] m

वृत्ताकार टेबल कवर की परिधि = \[\text{2}\] 𝜋𝑟 \[=\text{ 2}\times \text{3}.\text{14}\times \frac{1.5}{2}\] 

 \[=\text{ 4}.\text{71}\] m

इसलिए, आवश्यक किनारी की लम्बाई \[=\text{ 4}.\text{71}\] m

 \[\text{1}\] मीटर किनारी लगाने का व्यय = ₹ \[\text{15}\] 

इसलिए, \[\text{4}.\text{71}\] मीटर किनारी लगाने का व्यय \[=\text{ 15}\times \text{4}.\text{71 }=\] ₹ \[\text{7}0.\text{65}\] 

अतः, \[\text{4}.\text{71}\] मीटर किनारी लगाने का व्यय ₹ \[\text{7}0.\text{65}\] है। 

7: दी गई आकृति, व्यास के साथ एक अर्ध वृत्त है। उसका परिमापज्ञात कीजिए।

उत्तर:

व्यास = \[\text{1}0\] cm ∴त्रिज्या = \[\frac{10}{2}\] = \[\text{5}\] cm 

के अनुसार,

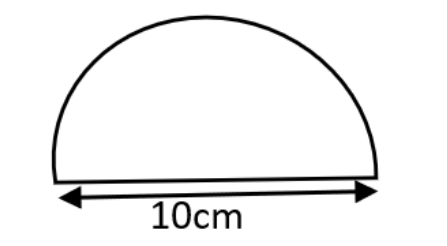
आकृति का परिमाप = अर्धवृत की परिधि + व्यास

 = πr + D 

 \[=\frac{22}{7}\times \text{5 }+\text{ 1}0\text{ }=\frac{110}{7}+\text{ 1}0\] 

 \[=\frac{\text{11}0+\text{7}0}{7}=\frac{180}{7}=\text{ 25}.\text{71}\] cm

अतः आकृति का परिमाप 25.71cm है।

8: ₹ \[\mathbf{15}\] प्रतिमीटर की दर से, \[\mathbf{1}.\mathbf{6}\] mव्यास वालेएक वृत्ताकार टेबलके ऊपर सतह परपॉलिशकराने का व्यय ज्ञात कीजिए।(𝜋 = \[\mathbf{3}.\mathbf{14}\] लीजिए)

उत्तर:

वृत्ताकार टेबल के ऊपरी सतह का व्यास = \[\text{1}.\text{6}\] m

∴ वृत्ताकार टेबल के ऊपरी सतह की त्रिज्या = \[\frac{1.6}{2}=\text{ }0.\text{8}\] cm

वृत्ताकार टेबल के ऊपरी सतह का क्षेत्रफल 

= $𝜋𝑟^2$ \[=\text{ 3}.\text{14}\times 0.\text{8}\times 0.\text{8 }=\text{ 2}.00\text{96}\] $m^2$

निया है: \[\text{1}\] $m^2$ पॉलिश करने का व्यय = ₹ \[\text{15}\] 

इसलिए, \[\text{2}.00\text{96}\] $m^2$

पॉलिश करने का व्यय \[=\text{ 15}\times \text{2}.00\text{96}\] 

 = ₹ \[\text{3}0.\text{14}\] (लगभग) 

अतः वृत्ताकार टेबल के ऊपरी सतह पर पॉलिश कराने का व्यय लगभग₹30.14है। 

9: शाईली \[\mathbf{44}\] cm लम्बाई वाली एक तार लेती हैऔर उसेएक वृत्तके आकार में मोड़ देती है। उस वृत्त की त्रिज्या ज्ञात कीजिए। इसकाक्षेत्रफल भी ज्ञात कीजिए।यदि इस तारको दोबारा एक वर्ग के आकार मेंमोड़ा जाता है, तोइसकी प्रत्येक भुजा की लम्बाई क्या होगी ?

उत्तर:

ताकि की कुल लम्बाई = \[\text{44}\] cm 

∴ वृत्त की परिधि = \[\text{2}\] 𝜋𝑟 = \[\text{44}\] cm 

 \[\text{2}\times \frac{22}{7}\times \text{ r }=\text{44}\] 

𝑟 \[=\frac{\text{44}\times \text{7}}{\text{2}\times \text{22}}=\text{ 7}\] cm

इसलिए, वृत्त का क्षेत्रफल = $𝜋𝑟^2$ =

 \[\frac{22}{7}\times \text{7}\times \text{7 }=\text{ 154}\] $cm^2$

जब तार को दोबारा एक वर्ग के आकार में मोड़ा जाता है, तो वर्ग का

परिमाप = \[\text{44}\] cm 

 \[\text{4}\] × भुजा = \[\text{44}\] 

भुजा = \[\frac{44}{4}=\text{ 11}\] cm

इसलिए, वर्ग का क्षेत्रफल = भुजा × भुजा = \[\text{11}\times \text{11 }=\text{ 121}\] $cm^2$

10: \[\mathbf{14}\] cm त्रिज्या वाली एक वृत्ताकार गत्तेकी शीट मेंसे, \[\mathbf{3}.\mathbf{5}\] cm त्रिज्या वाले दो वृत्त दोऔर \[\mathbf{3}\] cm लंबाई तथा \[\mathbf{1}\] cm चौड़ाई वाले एकआयत क निकाल दिया जाता है (जैसा की आकृति में दिखाया गया है)।शीट के शेष भाग का क्षेत्रफल ज्ञात कीजिए।

उत्तर:

वृत्ताकार गत्ते की शीट की त्रिज्या (R)= \[\mathbf{14}\] cm और छोटे वृत्त की त्रिज्या (r)= \[\text{3}.\text{5}\] cm 

आयत की लम्बाई (l) = \[\text{3}\] cm और 

आयत की चौड़ाई (b) = \[\text{1}\] cm 

के अनुसार, 

शीट के शेष भाग का क्षेत्रफल 

= वृत्ताकार भाग का क्षेत्रफल – (दो छोटे वृत्त का क्षेत्रफल +आयत काक्षेत्रफल) 

= 𝜋$𝑅^2$ − [2(𝜋𝑟$^2$) + (𝑙× 𝑏)] 

 \[=\frac{22}{7}\times \text{14}\times \text{14 }-\text{ }[(\text{2}\times \frac{22}{7}\times \text{3}.\text{5}\times \text{3}.\text{5})\text{ }-\text{ }(\text{3}\times \text{1})] \] 

 \[=\text{ 22}\times \text{14}\times \text{2 }-\text{ }[\text{44}\times 0.\text{5}\times \text{3}.\text{5 }+\text{ 3}] \text{ }=\text{ 616 }-\text{ 8}0\] 

 \[=\text{ 536}\] 𝑐$m^2$

11: \[\mathbf{6}\] cm भुजा वाले एक वर्गाकार एल्यूमिनियम शीट के टुकड़े में से \[\mathbf{2}\] cm त्रिज्या वाले एक वृत्त को काट दिया जाता है। शीट के शेष भाग का क्षेत्रफल ज्ञातकीजिए।(𝜋 = \[\mathbf{3}.\mathbf{14}\] लीजिए)

उत्तर:

वृत्त की त्रिज्या = \[\text{2}\] cm और 

वर्गाकार एल्यूमिनियम शीट की भुजा = \[\text{6}\] cm 

के अनुसार, 

शीट के शेष भाग का क्षेत्रफल 

= एल्यूमिनियम शीट का क्षेत्रफल – काटे गए वृत्त का क्षेत्रफल 

= भुजा × भुजा − π𝑟2

 \[=\text{6}\times \text{6 }-\frac{22}{7}\times \text{2}\times \text{2 }=\text{ 36 }-\text{ 12}.\text{56 }=\text{ 23}.\text{44}\] $cm^2$

अतः, शीट के शेष भाग का क्षेत्रफल \[\text{23}.\text{44}\] $cm^2$है।

12: एक वृत्त की परिधि \[\mathbf{31}.\mathbf{4}\] cm है। वृत्त की त्रिज्या औरक्षेत्रफलज्ञात कीजिए।(𝜋 = \[\mathbf{3}.\mathbf{14}\] लीजिए)

उत्तर:

वृत्त की परिधि = \[\text{31}.\text{4}\] cm 

 \[\text{2}\] 𝜋𝑟 = \[\text{31}.\text{4}\] 

 \[\text{2}\] × \[\text{3}.\text{14}\] × 𝑟 = \[\text{31}.\text{4}\] 

𝑟 \[=\frac{31.4}{\text{2}\times \text{3}.\text{14}}=\text{ 5}\] cm

इसलिए, वृत्त का क्षेत्रफल = $𝜋𝑟^2$ = \[\text{3}.\text{14}\times \text{5}\times \text{5 }=\text{ 78}.\text{5}\] $cm^2$

अतः, वृत्त की त्रिज्या तथा क्षेत्रफल क्रमशः \[\text{5}\] cm और \[\text{78}.\text{5}\] $cm^2$है।

(“Image will be updated soon”)

13: एक वृत्ताकारफूलों की क्यारी के चारोंऔर \[\mathbf{4}\] mचौड़ा पथ हैतथा फूलों की क्यारी का व्यास \[\mathbf{66}\] mहै। इस पथ का क्षेत्रफल ज्ञातकीजिए।(𝜋 = \[\mathbf{31}.\mathbf{4}\] लीजिए)

उत्तर:

फूलों की क्यारी का व्यास = \[\text{66}\] m

∴ वृत्ताकार फूलों की क्यारी की त्रिज्या (r) 

 \[=\frac{66}{2}=\text{ 33m}\] 

∴ \[\text{4}\] mचौड़े पथ के साथ क्यारी की त्रिज्या (r)

 \[=\frac{66}{2}=\text{ 33m}\] ानुसार, पथ का क्षेत्रफल 

= बड़ेवृत्त का क्षेत्रफल –छोटे वृत्त का क्षेत्रफल 

= 𝜋$𝑅^2$ − 𝜋$𝑟^2$ = 𝜋($𝑅^2$ − $𝑟^2$)

= 𝜋 \[\left[ {{\left( \text{37} \right)}^{\text{2}}}-\text{ }{{\left( \text{33} \right)}^{\text{2}}} \right] \] 

 \[=\text{3}.\text{14}\left[ \left( \text{37 }+\text{ 33} \right)\left( \text{37 }-\text{ 33} \right) \right] \] 

 \[=\text{3}.\text{14}\times \text{7}0\times \text{4 }=\text{ 879}.\text{2}0\] $m^2$

(“Image will be updated soon”)

अतः, पथ का क्षेत्रफल \[\text{879}.\text{2}0\] $m^2$ है।

14: एक वृत्ताकारफूलों के बगीचेका क्षेत्रफल \[\mathbf{314}\] $m^2$है। बगीचेकेकेंद्र मेंएक घुमने वाला फव्वारा (sprinkler) लगाया जाता है, जो अपने चारोंऔर \[\mathbf{12}\] mत्रिज्या के क्षेत्रफल मेंपानी का छिडकाव करता है। क्याफव्वारा पुरे बगीचेमें पानी का छिडकाव कर सकेगा ? (𝜋 = \[\mathbf{3}.\mathbf{14}\] लीजिए)

उत्तर:

फव्वारे द्वारा छिडकाव किए गए भाग का क्षेत्रफल 

=𝜋𝑟2 \[=\text{ 3}.\text{14}\times \text{12}\times \text{12 }=\text{ 452}.\text{16}\] $m^2$

वृत्ताकार फूलों के बगीचे का क्षेत्रफल= \[\text{314}\] $m^2$

यहाँ, वृत्ताकार फूलों के बगीचे का क्षेत्रफल, फव्वारे द्वारा छिड़काव किए गए क्षेत्रफल से कम है।

अतः, फव्वारा पूरे बगीचे में पानी का छिड़काव कर सकेगा। 

(“Image will be updated soon”)

15: आकृति में, अन्तः और बाह्य वृत्तो की परिधि ज्ञात कीजिए।(𝜋 = \[\mathbf{3}.\mathbf{14}\] लीजिए)

उत्तर:

बाह्य वृत्त की त्रिज्या (r) = \[\text{19}\] m

∴ बाह्य वृत्त की परिधि = \[\text{2}\]𝜋𝑟 \[=\text{ 2}\times \text{3}.\text{14}\times \text{9 }=\text{ 119}.\text{32}\] 𝑚

अब, अन्तः वृत्त की त्रिज्या (r’) = \[\text{19}-\text{1}0\text{ }=\text{ 9m}\] 

∴ अन्तः वृत्त की परिधि = \[\text{2}\] 𝜋𝑟′ \[=\text{ 2}\times \text{3}.\text{14}\times \text{9 }=\text{ 56}.\text{52}\] 𝑚

अतः, अन्तः वृत्त तथा वृत्त की परिधि क्रमशः \[\text{56}.\text{52}\] mऔर \[\text{119}.\text{32}\] mहैं।

16: \[\mathbf{28}\] cm त्रिज्या वाले एक पहिये \[\mathbf{352}\] mकी दुरीतय करने के लिए कितनीबार घुमाना पड़ेगा पड़ेगा ? (𝜋 = \[\frac{22}{7}\] लीजिए)

उत्तर: 16: 

माना, पहिये क 𝑛 बार घुमाना पड़ेगा।

पहिये की त्रिज्या = \[\text{28}\] cm और कुल दूरी = \[\text{352}\] m = \[\text{352}00\] cm 

∴ पहिये द्वारा तय की गई दूरी = 𝑛× पहिये की परिधि 

 \[\text{352}00\text{ }=\] 𝑛× \[\text{2}\] 𝜋𝑟

 \[\text{352}00\text{ }=\] 𝑛 \[\times \text{2}\times \frac{22}{7}\times \text{28}\] 

𝑛 = \[\frac{\text{352}00\times \text{7}}{\text{2}\times \text{22}\times \text{28}}\] 

𝑛 = \[\text{2}00\] चक्कर

अतः, पहिये को कुल दूरी तय करने के लिए \[\text{2}00\] बार घुमाना पड़ेगा।

17: एक वृत्ताकार घड़ी की मिनट की सुई की लम्बाई \[\mathbf{15}\] cm है।मिनट की सुई की नोक \[\mathbf{1}\] घंटेमें कितनी दुरी तय करती है? (𝜋 = \[\mathbf{3}.\mathbf{14}\] लीजिए)

उत्तर:

\[\text{1}\] घंटे में, मिनट की सुई की नोंक, एक सम्पूर्ण वृत्त बनती है। 

इस वृत्त की त्रिज्या (r) = \[\text{15}\] cm 

वृत्ताकार घड़ी की परिधि = \[\text{2}\] 𝜋𝑟 \[=\text{ 2}\times \text{3}.\text{14}\times \text{15 }=\text{ 94}.\text{2}\] 𝑐𝑚

अतः, मिनट की सुई की नोक \[\text{1}\] घंटे में \[\text{94}.\text{2}\] cm कुल दूरी तय करती है। 

ावली 11.4 

1: एक बगीचा \[\mathbf{90}\] mलंबा और \[\mathbf{75}\] m चौड़ा है। इसके बाहर, चारों और एक \[\mathbf{5}\] mचौड़ा पेड़ बनाना है। पथ का क्षेत्रफल ज्ञात कीजिए।बगीचे का क्षेत्रफल हेक्टेयर मेंभी ज्ञात कीजिए।

(“Image will be updated soon”)

उत्तर:

बगीचे की लम्बाई = \[\text{9}0\] m

बगीचे की चौड़ाई = \[\text{75}\] m

पथ सहित बगीचे की लम्बाई \[=\text{ 9}0+\text{5}+\text{5}=\text{1}00\text{m}\] 

पथ सहित बगीचे की चौड़ाई \[=\text{ 75}+\text{5}+\text{5}=\text{85m}\] 

पथ सहित बगीचे का क्षेत्रफल = लम्बाई × चौड़ाई

 \[=\text{ 1}00\times \text{85 }=\text{ 85}00\] $m^2$

केवल बगीचे का क्षेत्रफल = लम्बाई × चौड़ाई

 \[=\text{ 9}0\times \text{75 }=\text{ 675}0\] $m^2$

इसलिए, पथ का क्षेत्रफल 

= पथ सहित बगीचे का क्षेत्रफल केवल बगीचे का क्षेत्रफल 

 \[=\text{ 85}00\text{ }\text{ 675}0\text{ }=\text{ 175}0\] $m^2$

क्यूँकि, \[\text{1}\] $m^2$ = \[\frac{1}{10000}\] हेक्टेयर 

इसलिए, \[\text{6}, \text{75}0\] $m^2$ \[=\frac{6750}{10000}=\text{ }0.\text{675}\] हेक्टेयर

2: \[\mathbf{125}\] mलम्बाई और \[\mathbf{65}\] mचौड़ाई वालेआयताकारपार्क के चारोंऔरबाहर एक \[\mathbf{3}\] mचौड़ा पथ बना हुआ है। पथ का क्षेत्रफल ज्ञातकीजिए।

(“Image will be updated soon”)

उत्तर:

आयताकार की लम्बाई = \[\text{125}\] m

आयताकार पार्क की चौड़ाई = \[\text{65}\] m

पथ की चौड़ाई = \[\text{3}\] m

पथ सहित पार्क की लम्बाई \[=\text{125}+\text{3}+\text{3 }=\text{ 131m}\] 

पथ सहित पार्क की चौड़ाई \[=\text{ 65}+\text{3}+\text{3 }=\text{ 71m}\] 

∴ पथ का क्षेत्रफल 

=पथ सहित पार्क का क्षेत्रफल केवल पार्क का क्षेत्रफल

= (𝐴𝐵× 𝐴𝐷) − (𝐸𝐹 × 𝐸𝐻) \[=\text{ }(\text{131}\times \text{71})\text{ }-\text{ }(\text{125}\times \text{65})\] 

 \[=\text{ 93}0\text{1 }-\text{ 8125 }=\text{ 1}, \text{176}\] $m^2$

अतः, पथ का क्षेत्रफल \[=\text{ 1}, \text{176}\] $m^2$ है।

(“Image will be updated soon”)

3: \[\mathbf{8}\] cm लंबेऔर \[\mathbf{5}\] cm चौड़े एक गत्ते पर एक चित्र की पेंटिंग इस प्रकार बनाई गई है की इसकी प्रत्येक भुजाओ के अनुदिश \[\mathbf{1}.\mathbf{5}\] cm चौड़ा हाशिया छोड़ा गया है। हशीये का क्षेत्रफल ज्ञात कीजिए।

उत्तर:

पेंटिंग की लम्बाई = \[\text{8}\] cm 

पेंटिंग की चौड़ाई = \[\text{5}\] cm 

इसकी प्रत्येक भुजाओं के अनुदिश \[\text{1}.\text{5}\] cm चौड़ा हाशिया जोड़ा गया है।

पेंटिंग की लम्बाई में कमी \[=\text{ 8 }\text{ }\left( \text{1}.\text{5}+\text{1}.\text{5} \right)\text{ }=\text{ 8 }-\text{ 3 }=\text{ 5}\] cm 

पेंटिंग की चौड़ाई में कमी \[=\text{ 5 }\text{ }\left( \text{1}.\text{5}+\text{1}.\text{5} \right)\text{ }=\text{ 5 }\text{ 3 }=\text{ 2}\] cm 

∴ हाशीये का कुल क्षेत्रफल 

= गत्ते (ABCD) का क्षेत्रफल गत्ते (EFGH) का क्षेत्रफल

= (𝐴𝐵× 𝐴𝐷) − (𝐸𝐹 × 𝐸𝐻) \[=\text{ }(\text{8}\times \text{5})\text{ }-\text{ }(\text{5}\times \text{2})\] 

 \[=\text{ 4}0\text{ }-\text{ 1}0\text{ }=\text{ 3}0\] 𝑐$m^2$

अतः, हाशिये का कुल क्षेत्रफल \[\text{3}0\] $cm^2$ है। 

4: \[\mathbf{5}.\mathbf{5m}\] लंबे और \[\mathbf{4m}\] चौड़े कमरे के चारों और बाहर \[\mathbf{2}.\mathbf{25m}\] चौड़ा एक बरामदा बनाया गया है। ज्ञात कीजिए : 

(i) बरामदे का क्षेत्रफल

(ii) ₹ \[\mathbf{200}\] प्रति$m^2$ की दर से बरामदे के फर्श पर सीमेंट करने का व्यय।

(“Image will be updated soon”)

उत्तर:

(i) कमरे की लम्बाई = \[\text{5}.\text{5m}\] और 

कमरे की चौड़ाई = \[\text{4m}\] 

बरामदे सहित कमरे की लम्बाई \[=\text{ 5}.\text{5}+\text{2}.\text{25}+\text{2}.\text{25}=\text{1}0\text{m}\] 

बरामदे सहित कमरे की चौड़ाई \[=\text{ 4}+\text{2}.\text{25}+\text{2}.\text{25 }=\text{ 8}.\text{5m}\] 

बरामदे का क्षेत्रफल 

= बरामदे सहित कमरे का क्षेत्रफल – कमरे का क्षेत्रफल 

= ABCD का क्षेत्रफल – EFGH का क्षेत्रफल 

= (𝐴𝐵× 𝐴𝐷) − (𝐸𝐹 × 𝐸𝐻) \[=\text{ }(\text{1}0\times \text{8}.\text{5})\text{ }-(\text{5}.\text{5}\times \text{4})\] 

\[=\text{ 85 }-\text{ 22 }=\text{ 63}\] $m^2$

(ii) \[\text{1}\] $m^2$बरामदे के फर्श पर सीमेंट कराने का व्यय =₹ \[\text{2}00\] 

इसलिए, \[\text{63}\] $m^2$

बरामदे के फर्श पर सीमेंट कराने का व्यय 

 \[=\text{ 2}00\times \text{63 }=\] ₹ \[\text{12}, \text{6}00\] 

5: \[\mathbf{30}\] mभुजा वालेएक वर्गाकार बगीचेकी परिसीमा सेलगा भीतरकी और चौड़ा पथ बना हुआ है। ज्ञात कीजिए: 

(i) पथ का क्षेत्रफल

(ii) ₹ \[\mathbf{40}\] प्रति$m^2$ की दर सेबगीचेके शेष भाग पर घास लगवाने का व्यय।

(“Image will be updated soon”)

उत्तर:

(i) वर्गाकार बगीचे की भुजा = \[\text{3}0\text{m}\] और 

परिसीमा से लगे पथ की चौड़ाई = \[\text{1m}\] 

बिना पथ के, वर्गाकार बगीचे की भुजा \[=\text{ 3}0\text{ }\text{ }\left( \text{1}+\text{1} \right)\text{ }=\text{ 28m}\] 

इसलिए, पथ का क्षेत्रफल 

= ABCD का क्षेत्रफल – EFGH का क्षेत्रफल

= (𝐴𝐵× 𝐴𝐷) − (𝐸𝐹 × 𝐸𝐻) \[=\text{ }(\text{3}0\times \text{3}0)\text{ }-\text{ }(\text{28}\times \text{28})\] 

 \[=\text{ 9}00\text{ }-\text{ 784 }=\text{ 116}\] $m^2$

(ii) बगीचे के शेष भाग का क्षेत्रफल \[=\text{ 28}\times \text{28 }=\text{ 784}\] $m^2$

 \[\text{1}\] $m^2$ पर घास लगवाने का व्यय = ₹ \[\text{4}0\] 

 \[\text{784}\] $m^2$ पर घास लगवाने का व्यय 

 \[=\text{ 4}0\times \text{784 }=\] ₹ \[\text{31}, \text{36}0\] 

6: \[\mathbf{700}\] mलंबेऔर \[\mathbf{300}\] mचौड़ेएक आयताकारपार्क के मध्य सेहोकर जाते \[\mathbf{10}\] mचौड़े दो पथ बने हुए हैं जो एक दुसरे पर परस्पर लम्ब और चौपड के आकार के हैं। इमेंसे प्रत्येक पथ का क्षेत्रफल ज्ञात कीजिए तथा पार्क की भुजाओ को छोड़कर पार्क के शेष भाग का भी क्षेत्रफल ज्ञात कीजिए।अपने उत्तर:को हेक्टेयर में दीजिए।

(“Image will be updated soon”)

उत्तर:

यहाँ PQ = \[\text{1}0\] mऔर PS= \[\text{3}00\] m, EH =10 m और  EF = \[\text{7}00\] m

तथा KL = \[\text{1}0\] mऔर KN = \[\text{1}0\] m

दोनों पथो का क्षेत्रफल 

= PQRS का क्षेत्रफल + EFGH का क्षेत्रफल – KLMN का क्षेत्रफल

[KLMN को दो बार लिया गया है, इसलिए एक बार हटाया गया है ] 

= (𝑃𝑆× 𝑃𝑄) + (𝐸𝐹 × 𝐸𝐻) − (𝐾𝐿 × 𝐾𝑁)

 \[=\text{ }(\text{3}00\times \text{1}0)\text{ }+\text{ }(\text{7}00\times \text{1}0)\text{ }-\text{ }(\text{1}0\times \text{1}0)\] 

 \[=\text{ 3}000+\text{7}000-\text{1}00\text{ }=\text{ 99}00\] $m^2$

हम जानते है, \[\text{1}\] $m^2$ = \[\frac{1}{10000}\] हेक्टेयर

∴ \[\text{99}00\] $m^2$ = \[\frac{9900}{10000}=0.99\] हेक्टेयर

पार्क के शेष भाग का क्षेत्रफल = पार्क का क्षेत्रफल – पथों का क्षेत्रफल 

= (𝐴𝐵× 𝐴𝐷) \[-\text{99}00\]

 \[=\text{ }(\text{7}00\times \text{3}00)\text{ }-\text{ 99}00\] 

 \[=\text{ 2}, \text{1}0, 000\text{ }-\text{ 9}, \text{9}00\] 

 \[=\text{ 2}, 00, \text{1}00\] $m^2$

 \[=\frac{200100}{10000}\] हेक्टेयर

 \[=\text{ 2}0.0\text{1}\] हेक्टेयर 

7: \[\mathbf{90}\] m लम्बाई और \[\mathbf{60}\] m चौड़ाई वालेएक आयातकार मैदान मेंदो पथ बनाए गए हैं, जोभुजाओ के समांतर हैं, एक दसूरे के लंबवत काटते हैंऔरमैदान के मध्य सेह कि निकलतेहैं। यदि प्रत्येक पथ कीचौड़ाई \[\mathbf{3}\] m हो, तो ज्ञातकीजिए : 

(i) पथ द्वाराआच्छादितक्षेत्रफल।

(ii) ₹ \[\mathbf{110}\] प्रति$m^2$ की दर सेपथ बनाने का व्यय।

(“Image will be updated soon”)

उत्तर:

(i) यहाँ, PQ = \[\text{3}\] mऔर PS = \[\text{6}0\] m, EH = \[\text{3}\] mतथा 

EF = \[\text{9}0\] m, KL = \[\text{3}\] mऔर KN = \[\text{3}\] m

पथों का क्षेत्रफल 

= PQRS का क्षेत्रफल + EFGH का क्षेत्रफल – KLMN काक्षेत्रफल

= (𝑃𝑆× 𝑃𝑄) + (𝐸𝐹 × 𝐸𝐻) − (𝐾𝐿 × 𝐾𝑁)

 \[=\text{ }(\text{6}0\times \text{3})\text{ }+\text{ }(\text{9}0\times \text{3})\text{ }-\text{ }(\text{3}\times \text{3})\] 

 \[=\text{ 18}0\text{ }+\text{ 27}0\text{ }-\text{ 9 }=\text{ 441}\] $m^2$

(ii) 1 $m^2$पथ बनाने का व्यय = ₹ \[\text{11}0\] 

 इसलिए, \[\text{441}\] $m^2$

पथ बनाने का व्यय \[=\text{ 11}0\times \text{441}\] 

= ₹ \[\text{48}, \text{51}0\] 

8: प्रज्ञा \[\mathbf{4}\] cm त्रिज्या वाले एक वृत्ताकार पाइप के चारों और एक रस्सी लपेटती है (जैसा दिखाया गया है) और रस्सी की आवश्यक लम्बाई को काट लेतीहै। इसके बाद वह उसे \[\mathbf{4}\] cm भुजा वाले एक वर्गाकार बॉक्स के चारोंऔर लपेटती है। (दिखाया गया है) क्या उसके पास कुछ और रस्सी बचेगी ? (𝜋 = \[\mathbf{3}.\mathbf{14}\] लीजिए) 

(“Image will be updated soon”)

उत्तर:

वृत्ताकार पाइप की त्रिज्या = \[\text{4}\] cm 

पाइप के चारो और लपेटी गई रस्सी = \[\text{2}\] 𝜋𝑟 \[=\text{ 2}\times \text{3}.\text{14}\times \text{4}\] 

 \[=\text{ 25}.\text{12}\] 𝑐𝑚

इसलिए, वर्गाकार बॉक्स के चारो और लपेटी गई रस्सी \[=\text{ 4}\times \] भुजा

 \[=\text{ 4}\times \text{4 }=\text{ 16}\] 𝑐𝑚

बची हुई रस्सी

=

पाइप के चारों और लपेटी गई रस्सी −

वर्गाकार बॉक्स के चारों और लपेटी गई रस्सी \[=\text{ 25}.\text{12 }-\text{ 16}\] 

 \[=\text{ 9}.\text{12}\] cm

अतः, उसके पास \[\text{9}.\text{12}\] cm रस्सी बचेगी।

9: संलग्न आकृति, एक आयताकारपार्क के मध्य में एक वृत्ताकारफूलों की क्यारीको दर्शाती है। ज्ञात कीजिए : 

(i) पूरे पार्क का क्षेत्रफल

(ii) फूलों की क्यारी का क्षेत्रफल

(iii) फूलों की क्यारी को छोड़कर, पार्क के शेष भाग का क्षेत्रफल

(iv) क्यारी की परिधि

(“Image will be updated soon”)

उत्तर:

आयताकार पार्क की लम्बाई = \[\text{1}0\] m

आयताकार पार्क की चौड़ाई = \[\text{5}\] m

वृत्ताकार फूलों की क्यारी की त्रिज्या = \[\text{2}\] m

(i) आयताकार पार्क का क्षेत्रफल = लम्बाई × चौड़ाई

 \[=\text{ 1}0\times \text{5 }=\text{ 5}0\] $m^2$

(ii) फूलों की क्यारी का क्षेत्रफल $𝜋𝑟^2$ \[=\text{ 3}.\text{14}\times \text{2}\times \text{2}\] 

 \[=\text{ 12}.\text{56}\] $m^2$

(iii) फूलों की क्यारी को छोड़कर, पार्क के शेष भाग का क्षेत्रफल 

=

आयताकार पार्क का क्षेत्रफल −

वृत्ताकार फूलों की क्यारी का क्षेत्रफल \[=\text{ 5}0\text{ }-\text{ 12}.\text{56}\] 

 \[=\text{ 37}.\text{44}\] $m^2$

(iv) वृत्ताकार फूलों की क्यारी की परिधि = \[\text{2}\] 𝜋𝑟

 \[=\text{ 2}\times \text{3}.\text{14}\times \text{2 }=\text{ 12}.\text{56}\] 𝑚

10: दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए :

(“Image will be updated soon”)

उत्तर:

(i) यहाँ, AB = \[\text{18}\] cm, BC = \[\text{1}0\] cm, AF = \[\text{6}\] cm, AE = \[\text{1}0\] cm और BE = \[\text{8}\] cm 

छायांकित भाग का क्षेत्रफल 

= आयत ABCD का क्षेत्रफल − ( FAE का क्षेत्रफल +

 EBC का क्षेत्रफल)

= (AB × BC) − ( \[\frac{1}{2}\] × 𝐴𝐸 × 𝐴𝐹 + \[\frac{1}{2}\] × 𝐵𝐸 × 𝐵𝐶)

 \[=\text{ }(\text{18}\times \text{1}0)\text{ }-\text{ }(\frac{1}{2}\times \text{1}0\times \text{6 }+\text{ }\frac{1}{2}\times \text{8}\times \text{1}0)\] 

 \[=\text{ 18}0\text{ }-\text{ }\left( \text{3}0\text{ }+\text{ 4}0 \right)\] 

 \[=\text{ 18}0\text{ }-\text{ 7}0\text{ }=\text{ 11}0\] 𝑐$m^2$

(ii) यहाँ, SR = (SU+UR) = \[\text{2}0\] cm, QR = \[\text{2}0\] cm, PQ = SR = \[\text{2}0\] cm, 

 PT = PS –TS = \[\text{1}0\] cm, TS = \[\text{1}0\] cm, SU = \[\text{1}0\] cm 

QR = \[\text{2}0\] cm और UR = \[\text{1}0\] cm 

छायांकित भाग का क्षेत्रफल 

= वर्ग PQRS का क्षेत्रफल − ( QPT का क्षेत्रफल +

 TSU का क्षेत्रफल +  UQR का क्षेत्रफल)

= (𝑆𝑅× 𝑄𝑅) − ( \[\frac{1}{2}\] × 𝑃𝑄 × 𝑃𝑇 + \[\frac{1}{2}\] × 𝑆𝑇 × 𝑆𝑈 + \[\frac{1}{2}\] ×𝑈𝑅× 𝑄𝑅) \[=\text{ }(\text{2}0\times \text{2}0)-\text{ }(\frac{1}{2}\times \text{2}0\times \text{1}0\text{ }+\frac{1}{2}\times \text{1}0\times \text{1}0\text{ }+\text{ }\frac{1}{2}\times \text{2}0\times \text{1}0)\] .

 \[=\text{ 4}00\text{ }-\text{ 1}00\text{ }-\text{ 5}0\text{ }-\text{ 1}00\] 

 \[=\text{ 15}0\] 𝑐$m^2$

11: चतुर्भुजABCD का क्षेत्रफल ज्ञात कीजिए। यहाँ AC = \[\mathbf{22}\] cm, BM = \[\mathbf{3}\] cm, DN = \[\mathbf{3}\] cm और 𝐵𝑀⊥𝐴𝐶, 𝐷𝑁⊥𝐴𝐶है।

(“Image will be updated soon”)

उत्तर:

यहाँ, AC = \[\text{22}\] cm, BM = \[\text{3}\] cm, DN = \[\text{3}\] cm 

चतुर्भुज ABCD का क्षेत्रफल 

=  ABC का क्षेत्रफल +  ADC का क्षेत्रफल

= \[\frac{1}{2}\] × 𝐴𝐶 × 𝐵𝑀 + \[\frac{1}{2}\] × 𝐴𝐶 × 𝐷𝑁

 \[=\frac{1}{2}\times \text{22}\times \text{3 }+\frac{1}{2}\times \text{22}\times \text{3}\] 

 \[=\text{ 3}\times \text{11 }+\text{ 3}\times \text{11}\] 

 \[=\text{ 33 }+\text{ 33}\] 

 \[=\text{ 66}\] 𝑐$m^2$

अतः, चतुर्भुज ABCD का क्षेत्रफल \[\text{66}\] $cm^2$है।

NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area In Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 7 Maths Chapter 11 solution Hindi mediums are created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 7 Maths Chapter 11 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 7 Maths Chapter 11 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 7 Maths Perimeter and Area solution Hindi medium from Vedantu app as well by following similar procedures, but you have to download the app from the Google play store before doing that. 

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 7 Maths Perimeter and Area in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 7 can download these solutions at any time as per their convenience for self-study purposes. 

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/ solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, and illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 7 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.