




How to Find All Factors of 385 with Examples
Factors of 385 mean the numbers divided into 385 completely or without leaving any remainder. A prime number has only two positive factors, and a composite number has more than 2 positive factors. The number of factors of a number depends on the types of the given number.
We can use the factoring concept in real-life situations. Suppose you want to cut an iron string with a length of 385m into 4 equal parts without wasting iron. To check it, we will check whether 4 is a factor of 385 or not. If 4 is a factor of 385, then it is possible. Otherwise, it is not.
Number of Factors of 385
The unit digit of 385 is 5. So 385 is divisible by 5. In other words, 385 has a factor other than 1 and itself. It indicates that 385 is a composite number. Thus, the number of factors 385 is more than 2.
How to Find the Factors of 385?
First, we will find the least prime number that divides 385 evenly. Then the divisor is the factor of 385. Again we will find the least prime that divides the quotient evenly. The procedure will go until we get 1 as a quotient. Factor 385 is all divisors, quotients, and products of any prime divisor.
Step 1: Finding the smallest factor
Since 385 is an odd number, it is not divisible by 2 and 4.
The sum of the digits is 3+8+5 = 16, which is not divisible by 3. Thus 385 is not divisible by 385.
\[385 \div 5 = 77\]
So 5 and 77 are two factors of 385.
Step 2: Finding the smallest factor of the quotient which is 77.
77 is divisible by 7.
\[77 \div 7 =11\]
So 7 and 11 are two factors of 385.
Step 3: Finding the smallest factor of the quotient that is 11.
11 is a prime so it is divisible by 11 only.
\[11 \div 11 =1\]
So 11 is a factor of 385.
Step 4: Finding the product any two prime factors
\[5 \times 7 = 35\]
\[5\times 11 =55\]
\[7 \times 11 =77\]
The factor of 385 are 1,5,7,11,35,55,77 and 385.
Negative Factors of 385
\[385 \div (-1) = -385\]
\[385 \div (-5) = -77\]
\[385 \div (-7) = -55\]
\[385 \div (-11) = -35\]
\[385 \div (-35) = -11\]
\[385 \div (-55) = -7\]
\[385 \div (-77) = -5\]
All negative values of the factors of 385 divide 385 evenly. Thus the negative value of the factors is also a factor of 385.
Sum of Factors
All factors 385 are 1,5,7,11,35,55,77, 385, -1,-5,-7,-11,-35,-55,-77 and -385.
The sum of the factors is
1+5+7+11+35+55+77+385+( -1)+(-5)+(-7)+(-11)+(-35)+-(55)+(-77) =0
What are Factor Pairs?
Factor pairs of a number are a combination of two numbers in such a manner the product of the numbers is always the given number.
In other words, the factor pair of 385 is a product of two factors such that the product of the factors is 385.
The factors of 385 are 1,5,7,11,35,55,77, 385, -1, -5, -7, -11, -35, -55, -77 and -385.
\[1 \times 385 = 385\]
\[5 \times 77 = 385\]
\[7 \times 55 = 385\]
\[11 \times 35 = 385\]
\[-1 \times (-385) = 385\]
\[-5 \times (-77) = 385\]
\[-7 \times (-55) = 385\]
\[-11 \times (-35) = 385\]
The factor pairs are (1,385), (5,77), (7,55), (11,-35),(-1,-385), (-5,-77), (-7,-55), (-11,-35).
The Prime Factors of 385
The prime factorisation helps to find the prime factors of a number.
In this process, we divide the divisor by the smallest prime number until we get 1 as a quotient.
The factorization of 385 is \[5 \times 7 \times 11\].
What is a Factor Tree?
The factor tree of a number is used to find prime factors of a number. This is a pictorial format to define all prime factors of a number. In other words, the pictorial representation of prime factorisation.
The pictorial presentation of a prime factorisation of 385 is:
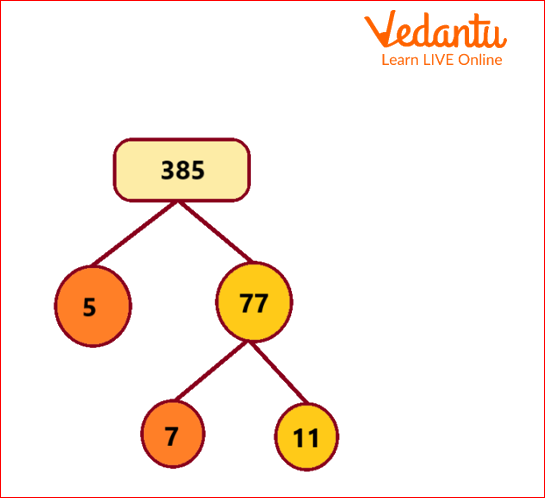
Factor tree of 385
The Least Common Positive Factor of 385 and Any Number
The common factor of two numbers is a number which is a factor of both numbers. The least common factor is the smallest common factor of both numbers.
The smallest factor of any number is 1.
Thus, the least common factor of 385 and any number is 1.
Interesting Facts
1 is the least common factor of any number.
Any number has at least two positive factors.
Solved Examples
Example 1: What is the sum of all the prime factors of 385?
Sol: The prime factors of 385 are 5, 7 and 11. So, the sum of all the prime factors of 385 are 5+7+11=23.
Example 2: Find the common factors of 385 and 147.
Sol:
The factor of 385 are \[1, 5,7,11, 5\times 7, 5\times 11, 7 \times 11, 1 \times 385\].
385 has the following factors: 385, 77, 55, 35, 11, 7, 5, 1.
The factor of 147 are \[1,3, 7,3\times 7, 7\times 7, 1 \times 147\].
147 has the following factors: 1, 3, 7, 21, 49, and 147.
Therefore, the common factors of 385 and 147 is 1 and 7.
Example 3: Find the sum of all factors of 385.
Sol: The factors of 385 are 385, 77, 55, 35, 11, 7, 5 and 1. The sum of all factors of 385 is 1+5+ 7+ 11+35+55+77+385= 576.
Conclusion
385 is a composite number rather than a prime number.
The composite number 385 has the following prime factors:
385 = 5 × 7 × 11The factors 385, 77, 55, 35, 11, 7, 5, 1 and the negatives -385, -77, -55, -35, -11, -7, -5, -1 all of these can exactly divide 385.
List of Related Articles
Practice Questions
Q 1: What is the product of the prime factors of 385?
Ans: 385
Q 2: What are the common factors in 385 and 55.
Ans: 1, 5, 11,55.
FAQs on Factors of 385 Explained
1: What is the number of positive factors of a prime?
A prime number is divisible by 1 and itself. The positive factors of a prime number are 1 and itself. Thus, the number of positive factors of a prime number are atleast 2.
2: What is the relation between factors and perfect square numbers?
If the prime factorization of a number can be written as \[N = X^2Y^2Z^2\] where X, Y, and Z are factors of N, then N is a perfect square number otherwise, the number is not a perfect square.
3: Is it possible that an even number has an odd factor?
We will check the given statement by using a counter-example.
14 is an even number.
2 | 14 |
7 | 7 |
1 |
The prime factorization of 14 is \[2 \times 7\].
14 has an odd number factor, i.e., 7 although 14 is an even number. Thus, it is possible that an even number has an odd factor.

















