




Step-by-Step Guide: How to Find the Factors of 318
Factor of a number is an integer that divides the given number evenly. A prime number has at least 4 (including negative factors) factors. A composite number has more than 4 factors. Now, coming to the main topic of our article, What are factors of 318? The answer is, a factor of 318 divides 318 evenly. If a number has multiple which is equal to 318 then the number is a factor of 318.
To answer our question, What are factors of 318? we need to discuss the factor of 318, what we truly mean is all the positive and negative whole numbers that can divide 318. The result of taking the number 318 and dividing it by one of its factors would be another factor of it.
Let's examine how to identify and list each of the 318 elements.
These numbers can be written as individual factors or factor pairs and can divide 318 into equal parts. We present them both ways. This is a specific number's mathematical decomposition.
How to Find the Factors of 318
The factor of 318 can be calculated by finding all divisors of 318 that divide completely. Since 318 is an even number, it is divisible by 2 and 2 is the least prime number.
\[318 \div 2 = 159\]
Thus 2 is a factor of 318.
Now find the least prime factor that divides quotients evenly.
159 is an odd number, thus it is not divisible by 2.
The sum of the digits is 1+5+9 = 15 which is divisible by 3.
Thus 159 is divisible by 3.
\[159 \div 3 =53\]
Thus 3 is a factor of 318.
Now 53 is a prime number, it is only divisible by 53.
\[53\div 53=1\]
Thus 53 is a factor of 318.
The product of any two factors is also a factor of 318.
Thus \[2 \times 3 = 6, 2\times 53 = 106, 3 \times 53 = 159\] are also a factor of 318.
A number is divisible by 1 and 318, thus 1 and 318 are factors of 318.
The factors of 318 are 1,2,3,6,53,106,159, and 318.
Negative Factors:
A negative integer can divide a positive number, but the quotient will be a negative number.
\[318 \div (-1) = -318\]
\[318 \div (-2) = -159\]
\[318 \div (-3) = -106\]
\[318 \div (-6) = -53\]
\[318 \div (-53) = -6\]
\[318 \div (-106) = -3\]
\[318 \div (-159) = -2\]
\[318 \div (-318) = -1\]
Thus -1,-2,-3,-6,-53,-106,-159, and -318 divides 318 evenly. Thus -1, -2, -3, -6, -53, -106, -159, and -318 are the factors of 318.
Prime Factorization:
Prime factorization of a number is a process to find prime factors of a number. To find factors of 318 by prime factorization, First we will divide 318 by the least prime that divides 318 evenly. In the same manner we divide quotients by least prime.
The product of prime numbers is 318. The prime factors of 318 by prime factorisation are 2,3,53.
Factor Tree of 318
Tree diagram is a pictorial representation of prime factorization of a number. It shows all prime factors of 318.
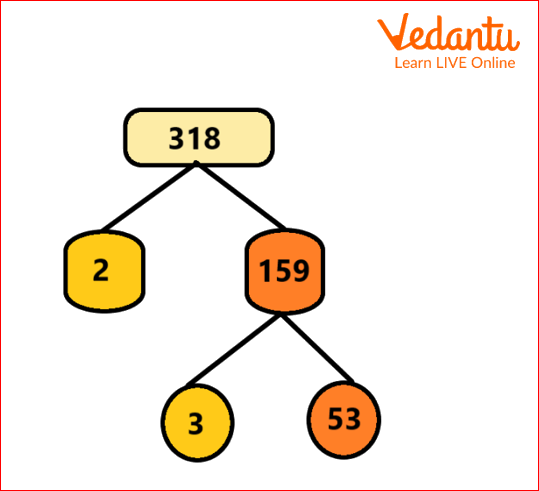
Factor tree of 318
Factor of 318 in Pairs
Factor pair looks like an ordered pair consisting of two elements. The number of factor pairs of numbers is equal to the half number of factors of a number. To find factor pairs, we will arrange the factors ascending and descending order. For the first factor pair:the first element will be the first number of ascending order and the second element will be the first element of descending order. For the second factor pair: the first element will be the second number of ascending order and the second element will be the second element of descending order. In the same manner we will find rest of them
Ascending order: 1,2,3,6,53,106,159,318
Descending order:318,159,106,53,6,3,2,1
Then the factors of 318 in pairs are (1, 318), (2, 159), (3, 106), (6, 53), (53, 6), (105, 3), (159, 2), (318, 1).
For negative factors
Ascending order:-318,-159,-106,-53,-6,-3,-2,-1
Descending order:-1,-2,-3,-6,-53,-106,-159,-318
(-318,-1),(-159,-2),(-105,-3),(-53,-6),(-6,-53),(-3,-106),(-2,-159),(-1,-318).
Order pairs are commutative. This means (a,b) = (b,a).
The order pairs are(1,318),(2,159),(3,106),(6,53), (-318,-1),(-159,-2),(-105,-3)and (-53,-6).
Number of Positive Factors:
The number of factors of a number depends on the exponent of prime factors of the given number. Assume N is a composite number and X, Y, and Z are prime factors of N such that \[N = X^aY^bZ^c\].
The formula of the number of positive factors of N is (a+1)(b+1)(c+1).
The prime factorization of 318 is \[2\times 3\times 53\].
Thus the number of positive factors of 318 is (1+1)(1+1)(1+1) = 8.
Sum of Factors:
The factors of 318 are 1,2,3,6,53,106,159,318,-1,-2,-3,-6,-53,-106,-159,-318.
Thus the sum of factors is 1+2+3+6+53+106+159+318+(-1)+(-2)+(-3)+(-6)+(-53)+(-106)+(-159)+(-318) =0
Solved Examples
Example 1: What is the sum of non prime factors of 318?
Sol: The prime factorization of 318 is
The prime factor of 318 is 2,3,53. The products of any two prime factors are \[2 \times 3 = 6, 2 \times 53 = 106, 3 \times 53 = 159\]. The negative value of the factors is also a factor of the number.
The factors of 318 are 1,2,3,6,53,106,159, 318,-1,-2,-3,-6,-53,-106,-159, -318.
The non prime factors are 6,106,159, 318,-1,-2,-3,-6,-53,-106,-159, -318.
The sum of the non prime factors are
6+106+159+318+(-1)+(-2)+(-3)+(-6)+(-53)+(-106)+(-159)+( -318) = -59.
Example 2: What is the sum of prime factors of 318?
Sol: The prime factorization of 318 is
The prime factor of 318 is 2,3,53. The sum of the prime factors is 2+3+53 = 59
Example 3: What is the highest factor of 318?
Sol: The prime factorization of 318 is
The prime factor of 318 is 2,3,53. The products of any two prime factors are \[2 \times 3 = 6, 2 \times 53 = 106, 3 \times 53 = 159\]. The negative value of the factors is also a factor of the number.
The factors of 318 are 1,2,3,6,53,106,159, 318,-1,-2,-3,-6,-53,-106,-159, -318.
The highest factor of 318 is 318.
Key Features about Number 318 and its Factors
318 is a composite number rather than a prime number.
The composite number 318 has the following prime factors:
\[318 = 2 \times 3 \times 53\]The factors 318, 159, 106, 53, 6, 3, 2, 1 and all the negatives -318, -159, -106, -53, -6, -3, -2, -1 all of these can exactly divide 318.
Conclusion
The factors of 318 are 318, 159, 106, 53, 6, 3, 2, 1,-318, -159, -106, -53, -6, -3, -2, -1. The prime factors of 318 are 2,3,53. As the number of positive factors is 8. Since the number of factors of 318 is more than 2, then 318 is a composite number.
List of Related Articles
Practice on Your Own
Q 1: What is the product of the two highest factors of 318?
Ans: 50562.
Q 2: What are the common factors in 318 and 87?
Ans: 1 and 3.
FAQs on Factors of 318 Explained with Examples
1. What are the factors of a number, explained with an example?
A factor is a whole number that divides another number exactly, leaving no remainder. For example, to find the factors of 12, we look for all numbers that divide 12 evenly. These are 1, 2, 3, 4, 6, and 12. Each of these is a factor of 12.
2. What are all the factors of 318?
The factors of 318 are all the whole numbers that can divide 318 without leaving a remainder. The factors are 1, 2, 3, 6, 53, 106, 159, and 318.
3. How can the factors of 318 be listed in pairs?
Factors can be listed in pairs that multiply together to give the original number. The factor pairs for 318 are:
1 × 318 = 318
2 × 159 = 318
3 × 106 = 318
6 × 53 = 318
4. What is the prime factorization of 318?
Prime factorization is the process of expressing a number as a product of its prime factors. For 318, we can find it using the division method:
Start by dividing 318 by the smallest prime number, 2: 318 ÷ 2 = 159.
Next, divide 159 by the next prime number, 3: 159 ÷ 3 = 53.
Since 53 is a prime number, we stop here.
Thus, the prime factorization of 318 is 2 × 3 × 53.
5. What is the main difference between factors and multiples?
The main difference lies in their relationship with a given number.
Factors are numbers that divide a given number exactly. The factors of a number are always less than or equal to the number itself and are finite. For example, the factors of 8 are 1, 2, 4, and 8.
Multiples are the result of multiplying a number by an integer. The multiples of a number are always greater than or equal to the number and are infinite. For example, the first few multiples of 8 are 8, 16, 24, 32, and so on.
6. Why is finding the prime factors of a number like 318 useful?
Finding the prime factorization of a number is a fundamental concept in mathematics with several important applications. For example, it is the most efficient way to:
Find the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of two or more numbers.
Simplify fractions to their lowest terms.
Understand the divisibility of a number.
Solve problems in cryptography and number theory.
7. How can you quickly check if 318 is divisible by common small numbers?
You can use divisibility rules as a shortcut to check for factors without performing long division:
For 2: A number is divisible by 2 if its last digit is even. The last digit of 318 is 8, so it is divisible by 2.
For 3: A number is divisible by 3 if the sum of its digits is divisible by 3. For 318, the sum is 3 + 1 + 8 = 12. Since 12 is divisible by 3, 318 is divisible by 3.
For 6: A number is divisible by 6 if it is divisible by both 2 and 3. Since 318 is divisible by both, it is also divisible by 6.
8. Is 318 a composite number? Why?
Yes, 318 is a composite number. A composite number is a whole number that has more than two factors (i.e., not just 1 and itself). Since the factors of 318 are 1, 2, 3, 6, 53, 106, 159, and 318, it has eight factors in total, which is more than two.
9. Why is the number 1 considered neither prime nor composite?
The number 1 is a special case and is considered neither prime nor composite. This is because:
A prime number must have exactly two distinct factors: 1 and itself. The number 1 only has one factor (itself).
A composite number must have more than two factors. The number 1 does not meet this condition.
This unique property is crucial for the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.























