




How to Find the Length and Properties of a Circle’s Chord
The line segment connecting any two points on a circle's circumference is known as the chord of a circle. A line segment which passes through the center of the circle is the longest chord of the circle which is known as diameter. In this article, we will learn about the chord of circle, the formula for a chord of circle, and its theorems. We will learn different words like ‘circumference ’, ‘diameter’, etc
What is the Chord of a Circle?
The line segment connecting any two points on a circle's circumference is known as the chord of a circle. So, the chord is one whose endpoints lie on the circumference. We can say that diameter is also the chord which is the longest and also passes through the center of the circle. The chord is one of the various line segments that may be made in a circle whose ends are on the circumference. A chord that runs through the center of the circle is also known as the diameter.
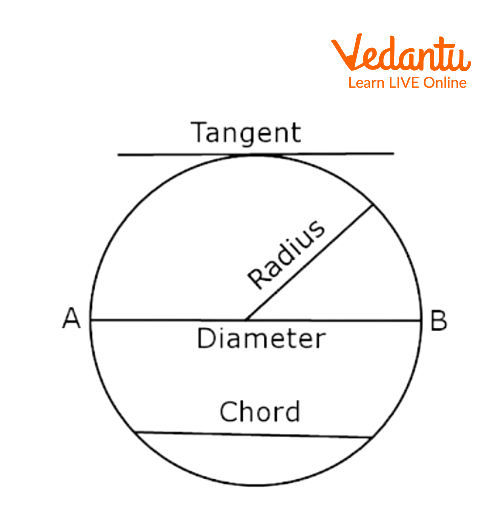
Keywords of a Circle
Properties of the Chord of a Circle
When a perpendicular is drawn to the chord from the center of the circle then it bisects the chord.
Chords of the circle which are equidistant from the center of the circle are equal.
When there are three collinear points then they pass through one and only one circle.
When we draw the chord of the circle, it divides the circle into two segments i.e. major segment and minor segment.
Well a secant is the one when the chord is extended infinity on both the sides.
Formula for the Chord Length of a Circle
Well there are two common formulas which are used to find the length of the chord. They are:
Using the Perpendicular Distance from the Center: The Chord Length is \[2\sqrt{{{r}^{2}}-{{d}^{2}}}\], where ‘r’ is the radius of the circle and ‘d’ is the perpendicular distance from the chord to the center of the circle.
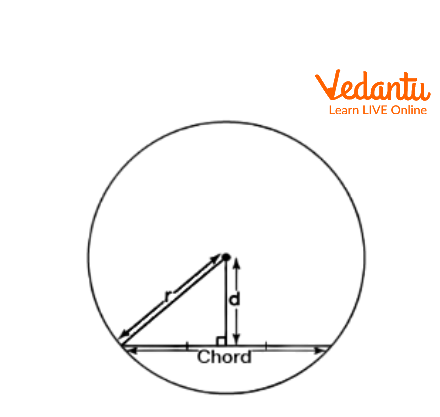
Perpendicular on the Chord of the Circle
Using Trigonometry: The Chord Length is \[2r\sin \left( {\frac{\theta }{2}} \right)\] , where ‘r’ is the circle's radius and ‘\[\theta \]’ is the angle subtended at the center by the chord.
Theorem of Unequal Chords
Statement: In a circle with two unequal chords, the larger chord will be closer to the center than the smaller chord.
Given: We have drawn chords CD and AB.
To prove that: The larger chord will be closer to the center.
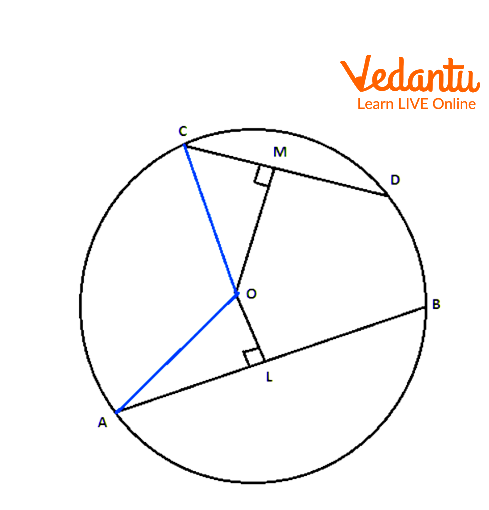
Two Unequal Chords
Proof:
We can see that, chord AB is near to the center and chord CD is away from the center. The length of the chord increases as it moves near to the center. Here, we can see that length of the chord AB is longer than the chord CD. This means, that we move away from the center the length of the chord decreases. From this, we can say that diameter is the longest chord.
Hence proved.
Theorem of Equal Chords, Equal Angles
Statement: At the circle's center, chords with identical lengths subtend equal angles.
Proof:
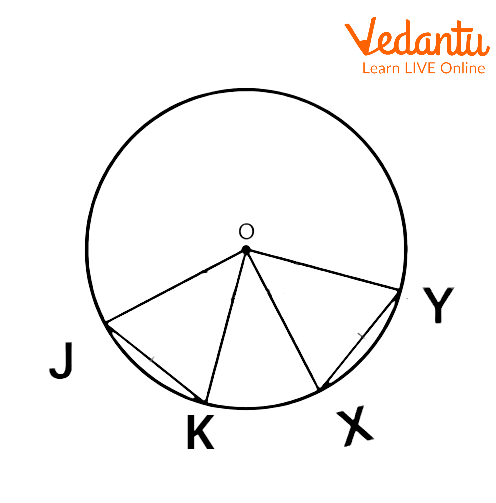
Equal chords
Given that \[O\] is a center.
\[JK\] and \[XY\] are equal chords of the circle.
That is, \[JK=XY\].
In \[\Delta \text{ }JOK\] and \[\Delta \text{ }XOY\],
Radii: \[OJ=OK=OX=OY\]
According to the SSS rule, two triangles are congruent if all three sides of one triangle are equal to the corresponding three sides of the second triangle.
So, \[\Delta \text{ }JOK\cong \Delta \text{ }XOY\]
By CPCT rule
\[\angle JOK=\angle XOY\]
Hence proved.
Converse Theorem of Equal Chords
Statement: The length of the chords is equal if and only if the angles of a circle's chords subtend are the same size.
Proof:
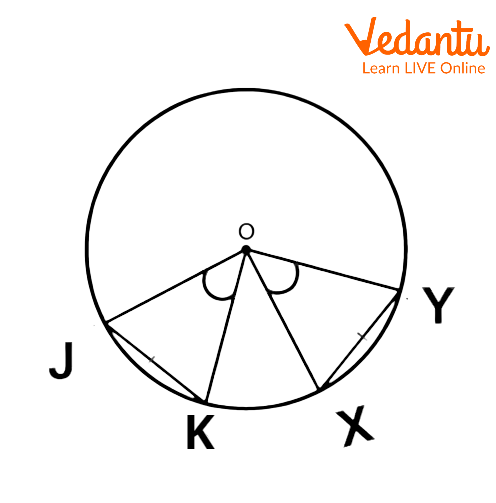
Converse Theorem of Equal Chords
Given that \[O\] is the center of the circle.
\[JK\]and \[XY\] are the chords that subtend equal angles at center \[O\].
So, \[\angle JOK=\angle XOY\]
In \[\Delta \text{ }JOK\] and \[\Delta \text{ }XOY\],
Radii: \[OJ=OK=OX=OY\]
According to the SAS rule, two triangles are said to be congruent if all two sides and one angle of one triangle are equal to the corresponding two sides and one angle of the second triangle.
So, \[\Delta \text{ }JOK=\Delta \text{ }XOY\]
By the CPCT rule,
\[JK=XY\]
Hence proved.
Interesting Facts
A circle's radius intersects the chord at a 90° angle.
Two radii join a chord's two ends to create an isosceles triangle.
The three provided non-collinear points are intersected by one and only one circle.
Solved Important Questions
1. We have a circle with center O and having 8 cm as the radius. Find the length of the chord if the length of the perpendicular drawn from the center is 10 cm.
Ans: Let AB be the chord of the circle with center O and let OM is perpendicular to the chord.
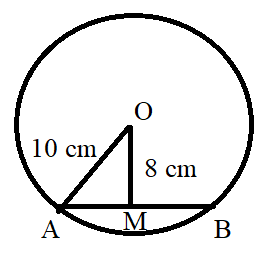
Given Length of Perpendicular
As we can see, triangle OMA is a right angled triangle. So by using Pythagoras theorem, we can say that,
\[\therefore O{A^2} = O{M^2} + A{M^2}\]
\[ \Rightarrow A{M^2} = O{A^2} - O{M^2}\]
\[ \Rightarrow A{M^2} = {10^2} - {8^2}\]
\[ \Rightarrow A{M^2} = 36\]
\[ \Rightarrow AM = 6\]
Also, we know that, Am = MB and AB = AM+MB = 6 + 6 = 12 cm
Thus, the length of the chord is 12 cm.
2. If a circle is formed when two points connected by a line segment subtend equal angles at two additional points located on the same side of the line as the line containing the line segment (i.e., they are concyclic). Is this statement true?
Ans: P, Q, R, and S are four points
PQ subtends equal angles at R and S
That is, \[\angle PR\text{Q=}\angle P\text{SQ}\]
We have to prove that P, Q, R, and S are cyclic
Since P, Q, and R, are non-collinear.
Consider, a circle passes through three collinear points
Let us draw a circle with the center at \[O\].

Points P, Q, R are Non-collinear
Let us assume it does not lie in the circle.
Angles within a segment are now equal.
\[\angle PR\text{Q=}\angle P\text{{S}'Q}\]—(1)
Given that,
\[\angle PR\text{Q=}\angle P\text{SQ}\]—(2)
From (1) and (2),
\[\angle P\text{{S}'Q}=\angle P\text{SQ}\]
In \[\Delta \text{ QS{S}'}\],
By exterior angle property
\[\angle P\text{{S}'Q}=\angle QS\text{{S}'+}\angle \text{{S}'}QS\]
From (1),
\[\angle P\text{SQ}=\angle P\text{SQ+{S}'}QS\]
\[\angle P\text{SQ-}\angle P\text{SQ={S}'}QS\]
\[\therefore \text{{S}'}QS=0\]
So, \[\text{{S}'}\] and \[S\] are coincide
Hence, our assumption was wrong.
Point \[S\] lies on circle
Thus, P, Q, R and S are concyclic.
Hence this statement is true.
3. Find the angle subtended by this chord at a point in the major segment if given that the chord of the circle is equal to its radius.
Ans: Let point O be the center of the circle and AB be the chord of the circle.
Also, we can see that OA and OB are the radii of the circle.
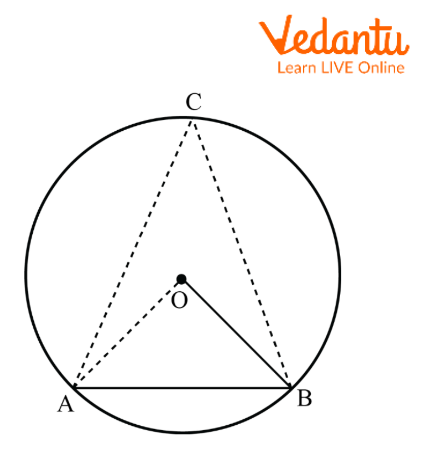
Chord is Equal to the Radius of Circle
Given that the chord of the circle is equal to the radius. This means AB = OA =OB.
Also, we can say that triangle AOB is an equilateral triangle.
\[\angle AOB = \angle OBA = \angle OAB = {60^ \circ }\]
As we know, the angle subtended by the arc at the center of the circle is twice the angle subtended by it at any other point in the remaining part of the circle.
\[\therefore \angle AOB = 2\angle ACB\]
\[ \Rightarrow \angle ACB = \frac{1}{2}\angle AOB\]
\[ \Rightarrow \angle ACB = \frac{1}{2}{60^ \circ } = {30^ \circ }\]
Hence, the angle subtended by the given chord at a point in the major segment is \[{30^ \circ }\].
Conclusion
In this article, we learned the chord meaning, chord Properties of a circle, the formula for the chord of a circle, its theorems and the chord of a circle example. The line segment connecting any two points on a circle's circumference is known as the chord of a circle. Note that the diameter (also known as chord of the circle) is the longest chord of a circle which passes through the center of the circle.
Practice Questions
1. Chord, meaning in Latin, is
A. Bowstring
B. String
C. Line
D. Group
2. When the chord's perpendicular distance from the circle's center is \[6\text{ }cm\] and the circle's radius is \[9\text{ }cm\], determine the chord's length.
A. \[13.014\text{ }cm\]
B. \[13.316\text{ }cm\]
C. \[13.4164\text{ }cm\]
D. \[13.2164\text{ }cm\]
3. Equation of chord
A. \[2\sqrt{{{r}^{2}}-{{d}^{2}}}\]
B. \[2\sqrt{r+d}\]
C. \[2\sqrt{{{r}^{2}}+{{d}^{2}}}\]
D. \[2\sqrt{r-d}\]
Answers:
1) A
2) C
3) A
FAQs on Chord of Circle: Key Concepts and Practice
1. What is a chord of a circle?
A chord of a circle is a straight line segment whose two endpoints both lie on the circumference of the circle. Unlike the radius or diameter, a chord does not necessarily have to pass through the center. Every diameter is a chord, but not every chord is a diameter.
2. What is the difference between a chord and the diameter of a circle?
The main difference lies in their relationship with the circle's center. A diameter is a special type of chord that must pass through the center of the circle. All other chords connect two points on the circumference but do not pass through the center. Consequently, the diameter is always the longest possible chord in any given circle.
3. How is the length of a chord calculated?
The length of a chord can be calculated using a few key methods, depending on the information given as per the CBSE 2025-26 syllabus:
Using Perpendicular Distance from Center: If you know the radius (r) and the perpendicular distance (d) from the center to the chord, you can use the Pythagorean theorem. The length of the chord is 2 × √(r² - d²).
Using the Angle Subtended at the Center: If you know the radius (r) and the angle (θ) that the chord subtends at the center, the length of the chord is given by the formula 2r × sin(θ/2).
4. What are the key properties of chords in a circle?
Chords have several important properties that are fundamental to circle geometry. The main properties are:
A line drawn from the center of a circle perpendicular to a chord bisects the chord.
The line joining the center of a circle to the midpoint of a chord is perpendicular to the chord.
Chords that are equal in length are equidistant (at the same distance) from the center.
Chords that are equidistant from the center are equal in length.
Equal chords of a circle subtend equal angles at the center.
5. Why is the diameter considered the longest chord of a circle?
The diameter is the longest chord because its length is exactly twice the radius (2r). For any other chord not passing through the center, a right-angled triangle can be formed with the radius as the hypotenuse, the perpendicular distance from the center as one side, and half the chord length as the other side. Since the hypotenuse (radius) is always the longest side in a right-angled triangle, half the chord length will always be less than the radius. Therefore, the full chord length will always be less than the diameter.
6. What happens when a perpendicular is drawn from the center of a circle to a chord?
When a perpendicular line is drawn from the center of a circle to any chord, it divides the chord into two equal halves. This is known as bisecting the chord. This property is one of the most critical theorems related to circles and is frequently used to find the length of a chord or its distance from the center.
7. How do equal chords relate to their distance from the circle's center?
There is a direct and reciprocal relationship. In a circle, if two chords are equal in length, they will be equidistant from the center. Conversely, if two chords are equidistant from the center, they must be equal in length. This property highlights the symmetry of a circle and is essential for proving congruency in problems involving chords.
8. Can a chord of a circle be longer than its radius? Explain why.
Yes, a chord can definitely be longer than the radius. The length of a chord can range from zero (when the two endpoints are the same) up to the length of the diameter (2r). Since the diameter is twice the radius, any chord whose length is between the radius (r) and the diameter (2r) is longer than the radius. For example, in a circle, a chord that forms the side of an inscribed equilateral triangle is longer than the radius (specifically, r√3).























