Cone Shape

What is a Cone?

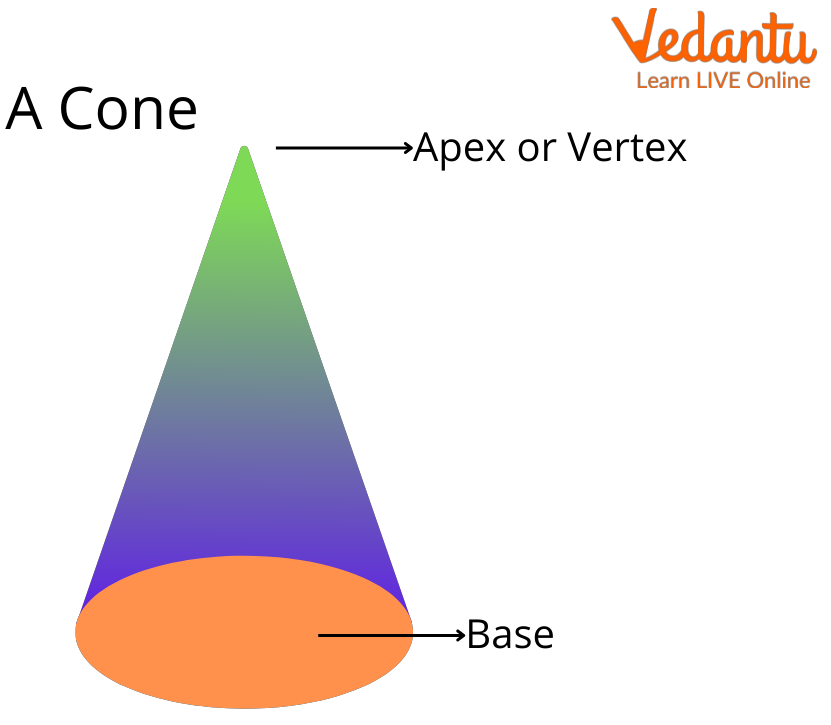
Do you like eating ice cream or wearing a birthday cap? Do you know they have something in common? Yes, these both have the same shape called the ‘cone.’ A cone shape is a three-dimensional geometric figure that has a curved surface, which is pointed towards the top. It is called the apex or vertex of a cone. The base of a cone has a flat circular surface. A cone has zero edges.

Are you excited to know more about this unique cone shape? Let us learn together about its types and properties, and we will also solve some questions.

Elements of the Cone Shape 

The three elements of the cone are:

1. Radius: The radius 'r' of a cone is the distance between the centre of the base of a cone to any point on the circumference of the base. 

2. Height: The height 'h' is the distance between the vertex of the cone and the centre of its base. 

3. Slant Height: It is the slanting length ‘l’ between the vertex of the cone shape and any point on the circumference of the base of a cone.

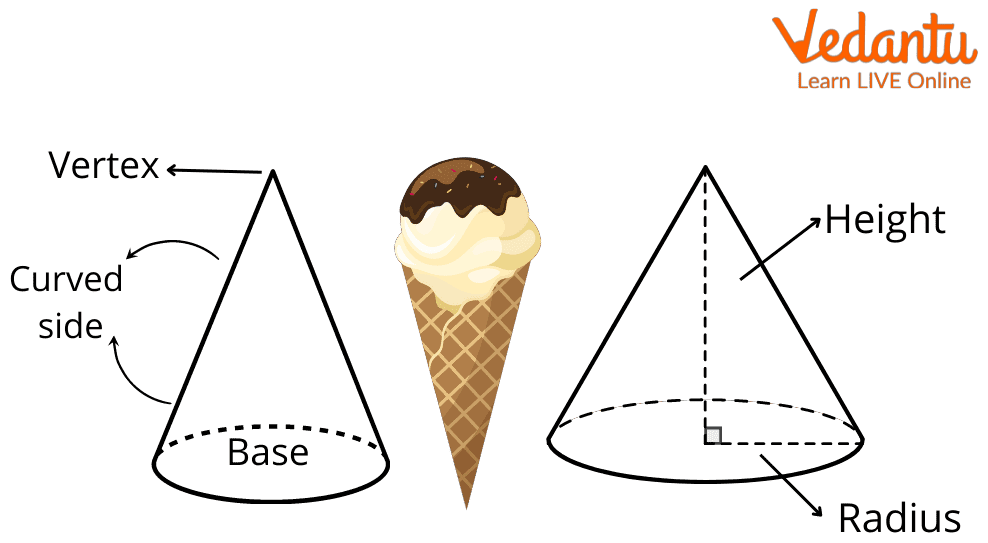
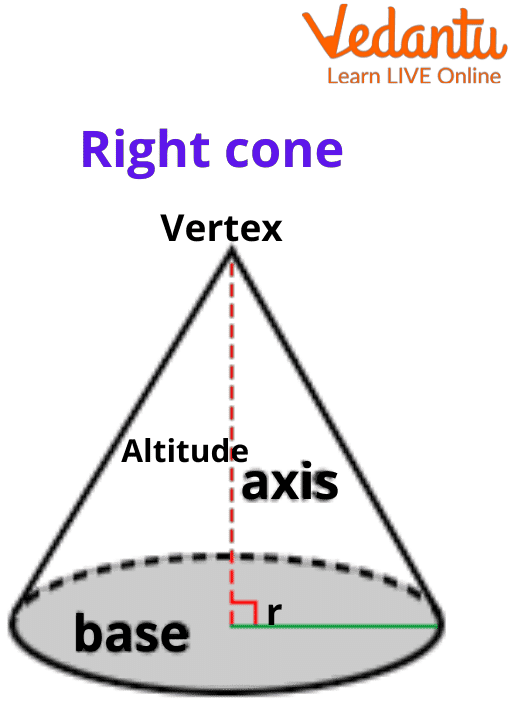
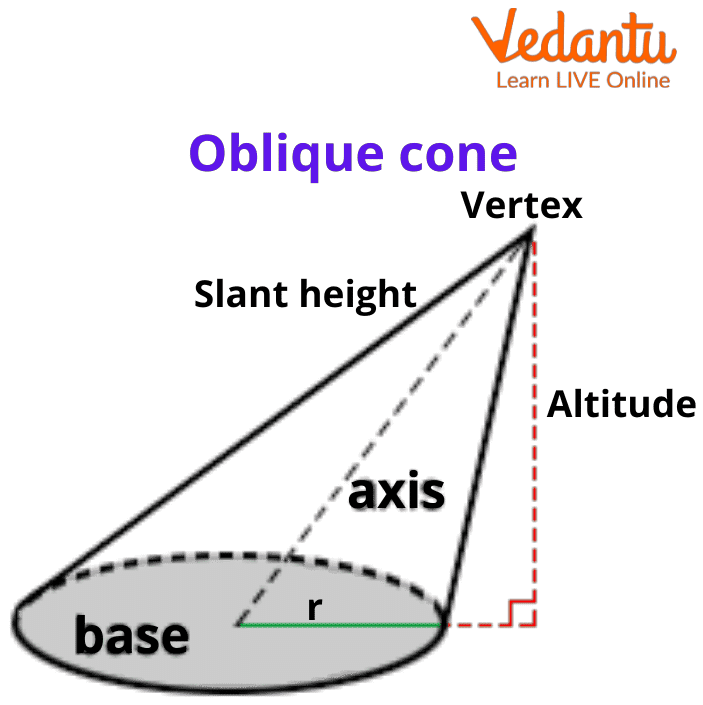
Types of Cones

A cone shape can be divided into two types, based on where its vertex is located. 

Right Circular Cone	Oblique Cone
In this type of cone, the vertex is perpendicular to the base and is exactly at the centre of the circular base of the cone.	In this type of cone, the position of the vertex is not directly above the centre of the circular base.
Therefore, the altitude or height of the cone forms a right angle with the base of the cone.	Therefore, the altitude or height of the cone does not form a right angle with the base of the cone.
This cone shape looks straight and is the most commonly used in geometry.	The oblique cone looks like a slanted cone or tilted cone.

Cone Formulas

For a cone shape with radius r, height h, and slant height l, its formulas are:

• The slant height of the cone = √(r2+h2).

• The total surface area of the cone = πr(l + r) square units.

• The curved surface area of the cone = πrl square units.

• The volume of the cone = ⅓ πr2h cubic units.

Cone Shape vs Other 3-D Shapes

If you are wondering why we are studying cone shape and what is so special about it? Here is your answer.

• A cone has only one flat face but all the other 3-D shapes have more than one or zero flat sides. A cylinder has two faces, while a sphere has none.

• A cone has one circular face and one flat surface, which is unlike any other figure.

• Cone is also the only shape that has one vertex. A pyramid has a vertex on its top that looks similar to that of the cone. But, a pyramid also has other vertices at its base). 

• Another characteristic of a cone shape is that we can not stack the cones, unlike other shaped things. We can only roll a cone.

Therefore, no other 3-D figure has exactly one face and one vertex.

Real-Life Examples of Cone Shape

Can you guess some things around us that have a cone shape? Here are some of them.

• An ice cream cone.

• A birthday cap.

• A Christmas tree.

• The orange-coloured traffic cones.

• Conical tents.

• A megaphone

Conclusion 

Did you enjoy learning about the cone? Isn’t it fun knowing that many things around us have a cone shape? Well, since the cone is one of the fundamental geometrical shapes, you must know all about it. But apart from cone shapes, you must also learn about other geometrical shapes, which are available at our website. 

Visit our website to learn different concepts of maths in a very interesting manner. So, what are you waiting for? Explore all the resources with just a click.