Question

Wind is blowing west to east along two parallel railway tracks. Two trains moving with the same speed in opposite directions have the steam track of one double that of the other. The speed of each train is
(A) Equal to that of the wind
(B) Three times that of the wind
(C) Double that of the wind
(D) Half that of the wind

Answer 1

Hint Draw the length of the first steam track as $2x$, and the second stream track as $x$. Now the first steam track is supported by both the train and the wind velocities and is therefore longer. The second steam track is of the train moving at the same speed in the opposite direction, and is opposed by the wind. We will use the distance formula to compute the speed of each train.

Complete Step by step answer

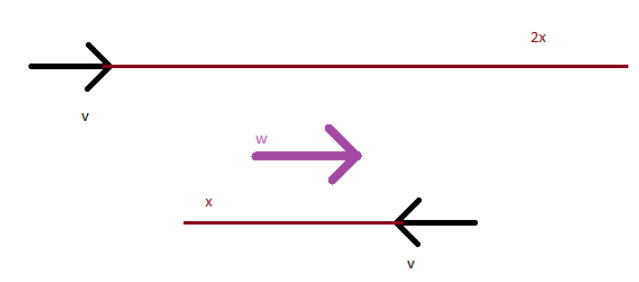
As shown in the above diagram, the steam track length is drawn in brown.
We will consider the speed of the trains as $v$ each, and the speed of the wind blowing as $w$.
The wind will be supporting the steam to spread and is shown in purple in the diagram.
So, from the first diagram, we get the equation as $v + w = \dfrac{{2x}}{t}$.
Here we assume that the steam length per unit time is equal to the speed of the train and the speed of the wind combined, since both are assisting it.
From the second diagram, we get the equation as $v - w = \dfrac{x}{t}$.
Here we assume that the steam length per unit time is equal to the speed of the train minus the speed of the wind combined, since the length direction is in the direction of the velocity of the train. In this assumption, it is noted that the wind speed is less than the speed of the train as per the diagram, which can be otherwise.
From the above two equations, we get
$v + w = 2(v - w)$
$ \Rightarrow v = 3w$.
Thus, the speed of the train which is $v$, is thrice the speed of the wind, $w$.

Therefore, the correct answer is option (2) Three times that of the wind.

Note: Here we have assumed simply that the steam track is of a certain length and that the wind and train speeds are acting for or against changing the length of the steam track. Therefore the simple equation of speed has been used.