Question

Which of the following graphs shows the variation of magnetic induction B with distance r from a long wire carrying current.
A.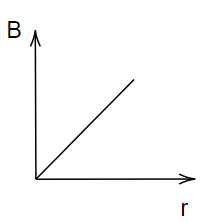
B.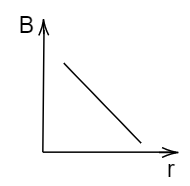
C.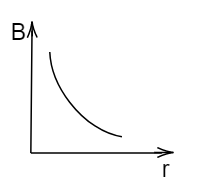
D.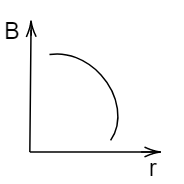

Answer 1

Hint:Before going to answer this question, let’s know about the ampere’s circuital law. This law states that the line integral of a magnetic field around any closed path is equal to the \[{\mu _0}\] times the total current passing through the closed loop. Ampere’s circuital law relates between the current and the magnetic field.

Formula Used:
The ampere’s circuital law is,
\[\oint {B \cdot dl = {\mu _o}I} \]
Where, B is magnetic field, dl is length element, I is current and \[{\mu _o}\] is permeability of free space.

Complete step by step solution:
We have an infinitely long current-carrying wire, we need to find the variation of the magnetic field with respect to r. If r is the distance from the wire increases then how the magnetic field varies. At a distance r if we assume a loop around the wire, then we can find the magnetic field. This can be found using the ampere’s circuital law i.e.,
\[\oint {B \cdot dl = {\mu _o}I} \]
\[\Rightarrow B\oint {dl = {\mu _o}I} \]
Where I is the current and dl is the circumference of the circular loop\[ = 2\pi r\]
\[B\left( {2\pi r} \right) = {\mu _o}I\]
\[\Rightarrow B = \dfrac{{{\mu _o}I}}{{2\pi r}}\]
\[\therefore B \propto \dfrac{1}{r}\]
From this equation, we can say that the magnetic field is inversely proportional to r, that is, as the r value increases the magnetic field decreases.

Hence, option C is the correct answer.

Additional information: The applications of ampere’s circuital law are as follows
1. Used to find the magnetic induction due to a long current-carrying wire and also for a long current carrying cylinder.
2. In order to find the magnetic field inside a toroid
3. To determine the magnetic field inside the conductor.
4. Used to find the forces between currents.

Note: Here, in this question it is important to remember the equation of ampere’s circuital law and how the distance influences the magnetic field. Using this it will be easier to find the solution.