
Uniform electric field of magnitude $100V{m^{ - 1}}$ in space is directed along the line $y = 3 + x$. Find the potential difference between point $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$.
A) $100V$
B) $200\sqrt 2 V$
C) $200V$
D) $0$
Answer
233.1k+ views
Hint: To solve this question we have to first plot the line $y = 3 + x$ . We can easily find the y-intercept and slope of the lone by comparing it with the standard equation. After that we can convert the electric field into its vector form. Also we have to find the position vector of AB. We can then use the electric field and the position vector to find potential differences.
Formulae used:
$y = mx + c$
Where $y$ is the Y-coordinate, $m$ is the slope of the line, $x$ is the X-coordinate of the line and $c$ is the y-intercept of the line.
$\vec r = \left( {{x_2} - {x_1}} \right)\hat i + \left( {{y_2} - {y_1}} \right)\hat j$
Here $\vec r$ is the position vector and $\left( {{x_1},{y_1}} \right)$and $\left( {{x_2},{y_2}} \right)$are the coordinates of two points.
$V = \vec E.\vec r$
Here $V$ potential difference between two points, $\vec E$ is the electric field vector and $\vec r$ is the position vector.
Complete step by step solution:
In the question equation of a straight line is given.
$y = 3 + x$
Let it be equation 1.
We know that,
$y = mx + c$
Where $y$ is the Y-coordinate, $m$ is the slope of the line, $x$ is the X-coordinate of the line and $c$ is the y-intercept of the line.
Comparing equation 1 with the equation of a straight line, we get
$ \Rightarrow m = 1 = \tan 45^\circ $ and
$ \Rightarrow c = 3$
Using the above values, we can plot the line
It's said in the question that that electric field is in the direction of the given line.
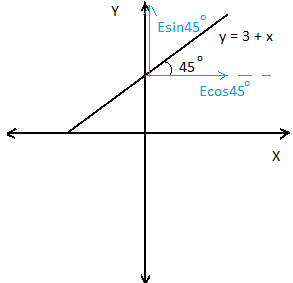
So the components of the electric field will be,
$ \Rightarrow \vec E = \left| E \right|\cos 45\hat i + \left| E \right|\sin 45\hat j$
Putting the value of $\left| E \right|$ in the above equation we get,
$ \Rightarrow \vec E = 100\cos 45\hat i + 100\sin 45\hat j$
$ \Rightarrow \vec E = 100 \times \dfrac{1}{{\sqrt 2 }}\hat i + 100 \times \dfrac{1}{{\sqrt 2 }}\hat j$
$ \Rightarrow \vec E = \dfrac{{100}}{{\sqrt 2 }}\hat i + \dfrac{{100}}{{\sqrt 2 }}\hat j$
In the question, it's given that we have found the potential difference between point $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$. So the position vector will be,
$ \Rightarrow \vec r = \left( {{x_2} - {x_1}} \right)\hat i + \left( {{y_2} - {y_1}} \right)\hat j$
Here $\vec r$ is the position vector and $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the coordinates of two given points.
Substituting the value of the coordinates at point $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$ we get,
$ \Rightarrow \vec r = \left( {1 - 3} \right)\hat i + \left( {3 - 1} \right)\hat j$
$ \Rightarrow \vec r = - 2\hat i + 2\hat j$
So applying the formulae
$ \Rightarrow V = \vec E.\vec r$
Where $V$ potential difference between two points, $\vec E$ is the electric field vector and $\vec r$ is the position vector, we get,
$ \Rightarrow V = \left( {\dfrac{{100}}{{\sqrt 2 }}\hat i + \dfrac{{100}}{{\sqrt 2 }}} \right).\left( { - 2\hat i + 2\hat j} \right)$
$ \Rightarrow V = \left( {\dfrac{{100}}{{\sqrt 2 }} \times - 2} \right) + \left( {\dfrac{{100}}{{\sqrt 2 }} \times 2} \right) = - \dfrac{{200}}{{\sqrt 2 }} + \dfrac{{200}}{{\sqrt 2 }} = 0$
Hence the electric field between the points $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$ will be zero.
Hence option (D) is the correct option.
Note: The electric field can be defined as the gradient of potential difference. It is a vector quantity. So always remember to write it in vector form while solving. Also be careful with the directions. The potential difference also called as voltage is directly proportional to the magnitude of uniform electric field. This is true only for uniform electric fields and if the field was not uniform then this proportionality will not be valid.
Formulae used:
$y = mx + c$
Where $y$ is the Y-coordinate, $m$ is the slope of the line, $x$ is the X-coordinate of the line and $c$ is the y-intercept of the line.
$\vec r = \left( {{x_2} - {x_1}} \right)\hat i + \left( {{y_2} - {y_1}} \right)\hat j$
Here $\vec r$ is the position vector and $\left( {{x_1},{y_1}} \right)$and $\left( {{x_2},{y_2}} \right)$are the coordinates of two points.
$V = \vec E.\vec r$
Here $V$ potential difference between two points, $\vec E$ is the electric field vector and $\vec r$ is the position vector.
Complete step by step solution:
In the question equation of a straight line is given.
$y = 3 + x$
Let it be equation 1.
We know that,
$y = mx + c$
Where $y$ is the Y-coordinate, $m$ is the slope of the line, $x$ is the X-coordinate of the line and $c$ is the y-intercept of the line.
Comparing equation 1 with the equation of a straight line, we get
$ \Rightarrow m = 1 = \tan 45^\circ $ and
$ \Rightarrow c = 3$
Using the above values, we can plot the line

It's said in the question that that electric field is in the direction of the given line.

So the components of the electric field will be,
$ \Rightarrow \vec E = \left| E \right|\cos 45\hat i + \left| E \right|\sin 45\hat j$
Putting the value of $\left| E \right|$ in the above equation we get,
$ \Rightarrow \vec E = 100\cos 45\hat i + 100\sin 45\hat j$
$ \Rightarrow \vec E = 100 \times \dfrac{1}{{\sqrt 2 }}\hat i + 100 \times \dfrac{1}{{\sqrt 2 }}\hat j$
$ \Rightarrow \vec E = \dfrac{{100}}{{\sqrt 2 }}\hat i + \dfrac{{100}}{{\sqrt 2 }}\hat j$
In the question, it's given that we have found the potential difference between point $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$. So the position vector will be,
$ \Rightarrow \vec r = \left( {{x_2} - {x_1}} \right)\hat i + \left( {{y_2} - {y_1}} \right)\hat j$
Here $\vec r$ is the position vector and $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the coordinates of two given points.
Substituting the value of the coordinates at point $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$ we get,
$ \Rightarrow \vec r = \left( {1 - 3} \right)\hat i + \left( {3 - 1} \right)\hat j$
$ \Rightarrow \vec r = - 2\hat i + 2\hat j$
So applying the formulae
$ \Rightarrow V = \vec E.\vec r$
Where $V$ potential difference between two points, $\vec E$ is the electric field vector and $\vec r$ is the position vector, we get,
$ \Rightarrow V = \left( {\dfrac{{100}}{{\sqrt 2 }}\hat i + \dfrac{{100}}{{\sqrt 2 }}} \right).\left( { - 2\hat i + 2\hat j} \right)$
$ \Rightarrow V = \left( {\dfrac{{100}}{{\sqrt 2 }} \times - 2} \right) + \left( {\dfrac{{100}}{{\sqrt 2 }} \times 2} \right) = - \dfrac{{200}}{{\sqrt 2 }} + \dfrac{{200}}{{\sqrt 2 }} = 0$
Hence the electric field between the points $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$ will be zero.
Hence option (D) is the correct option.
Note: The electric field can be defined as the gradient of potential difference. It is a vector quantity. So always remember to write it in vector form while solving. Also be careful with the directions. The potential difference also called as voltage is directly proportional to the magnitude of uniform electric field. This is true only for uniform electric fields and if the field was not uniform then this proportionality will not be valid.
Recently Updated Pages
JEE Main 2026 Session 2 Registration Open, Exam Dates, Syllabus & Eligibility

JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

Trending doubts
JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Why does capacitor block DC and allow AC class 12 physics JEE_Main

Understanding Average and RMS Value in Electrical Circuits

Understanding Collisions: Types and Examples for Students

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

CBSE Class 12 Physics Set 2 (55/2/2) 2025 Question Paper & Solutions

Inductive Effect and Its Role in Acidic Strength

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Units and Measurements Mock Test for JEE Main 2025-26 Preparation

Chemistry Question Papers for JEE Main, NEET & Boards (PDFs)




