Question

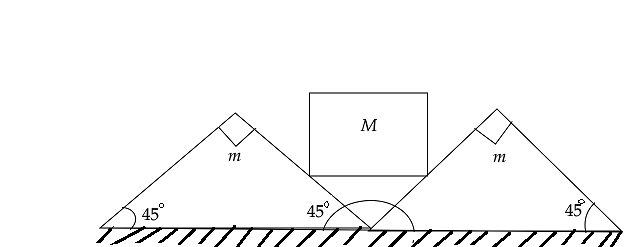
Two wedges, each of mass \[m\], are placed next to each other on a flat horizontal floor. A cube of mass $M$ is balanced on the wedges as shown in the figure. Assume no friction between the cube and the wedges, but a coefficient of static friction $\mu < 1$ between the wedges and floor, what is the largest M that can be balanced as shown without motion of the wedges?

A) $\dfrac{m}{{\sqrt 2 }}$
B) $\dfrac{{\mu m}}{{\sqrt 2 }}$
C) $\dfrac{{\mu m}}{{1 - \mu }}$
D) $\dfrac{{2\mu m}}{{1 - \mu }}$

Answer 1

Hint: We choose the usual force that works between the target and the floor here. Assume a normal force value, then calculate the coefficient of friction and. Multiply these values by each other. To find the friction, we separate the sections of the picture.


Formula used:
Friction of the wedge
\[f = \mu \left( {N\cos \theta + mg} \right)\]
Where,
$f$ is the friction the wedge of the floor is $mg$
$N$ is normal force
$\mu $ is the characteristics of the surface.

Complete step by step solution:
Given by,
Let mass \[m\], on a flat horizontal floor. A cube of mass $M$ is balanced on the wedges.
We find the motion of the wedges.
Now we assume that,
$2N\cos \theta = Mg$
Therefore the $\theta = {45^ \circ }$
The body parts of the above diagram is given below,
Here,
We know that,
$\sqrt {2N} = Mg$
Rearranging the given equation,
$N = \dfrac{{Mg}}{{\sqrt 2 }}$………..$(1)$
According to the formula of friction wedge
$\Rightarrow$ \[f = \mu \left( {N\cos \theta + mg} \right)\]
Then,
Substituting the given value
We get,
$\Rightarrow$ \[f = \mu \left( {\dfrac{{Mg}}{{\sqrt 2 }} \times \dfrac{1}{{\sqrt 2 }} + mg} \right)\]
Simplifying the friction,
$\Rightarrow$ \[f = \mu g\left( {\dfrac{M}{{\sqrt 2 }} + m} \right)\]
Now the wedge is balanced then
$\Rightarrow$ $F = N\sin \theta $……………$(2)$
Substituting the value of $N$ and $\theta $ in $(2)$ equation,
We get,
$\Rightarrow$ $F = \dfrac{{Mg}}{{\sqrt 2 }}\sin {45^ \circ }$
On simplifying,
$\Rightarrow$ $F = \dfrac{{Mg}}{2}$
Here,
$\Rightarrow$ $\dfrac{{\mu Mg}}{2} + \mu mg = \dfrac{{Mg}}{{\sqrt 2 }}$
Then,
 Rearranging the equation,
$\Rightarrow$ $\mu mg = \dfrac{{Mg}}{{\sqrt 2 }} - \dfrac{{\mu Mg}}{2}$
Here, We get,
$\Rightarrow$ $M = \dfrac{{2\mu m}}{{\left( {1 - \mu } \right)}}$

Hence, The option D is the correct answer.

Note: One needs to slip on all three surfaces when we weigh the wedges in order to move. The direction of the friction force will counteract the slipping on each surface. A plane's angle to the horizontal is just starting to slide when a body put on the plane begins to slide. The coefficient of static friction is the tangent of the friction angle.