Question

Two uniform rods of equal length but different masses are rigidly joined to form an L – shaped body, which is then pivoted as shown. If in equilibrium the body is in the shown configuration, ratio $\dfrac{M}{m} $ will be:

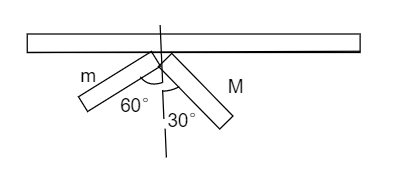
(A) $2 $
(B) $3 $
(C) $\sqrt 2 $
(D) $\sqrt 3 $

Answer 1

Hint A body attains equilibrium only when the force acting on the body along the x-axis and along the y-axis are balanced and the torque acting on the body is balanced i.e. clockwise torque is equal to the anti-clockwise torque acting on the body.

Formula used:
 $\overrightarrow \tau = \overrightarrow r \times \overrightarrow F $
Where $\overrightarrow \tau $ is the torque vector, $\overrightarrow r $ is the distance vector joining the axis of rotation and force vector, $\overrightarrow F $ is the force vector.

Complete step-by-step answer

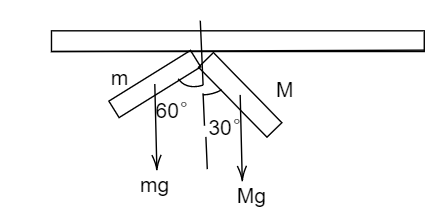
We know that,
A body attains equilibrium only when the force acting on the body along the x-axis and along the y-axis are balanced and torque acting on the body is balanced i.e. clockwise torque is equal to the anti-clockwise torque acting on the body.
From looking at the figure we can say that the force acting along the x-axis and the y-axis are balanced by the hinge force and gravitational force.
It is given that the body has attained equilibrium thus,
Clockwise torque will be equal to the anticlockwise torque.
By looking at the figure and using the formula,
  $\overrightarrow \tau = \overrightarrow r \times \overrightarrow F $
Where $\overrightarrow \tau $ is the torque vector, $\overrightarrow r $ is the distance vector joining the axis of rotation and force vector, $\overrightarrow F $ is the force vector.
As it is given that both the rods are of equal length and the gravitational force acting on a body can be considered acting on a single point which is the center of mass as both the rods are uniform their geometrical center is the same as the center of mass.
The clockwise torque is,
 ${\tau _{clockwise}} = Mg \times \dfrac{l}{2} \times \sin (30^\circ ) $
The anti-clock wise torque is,
 ${\tau _{anticlockwise}} = mg \times \dfrac{l}{2} \times \sin (60^\circ ) $
As
 $ \Rightarrow {\tau _{clockwise}} = {\tau _{anticlockwise}} $
Hence
\[ \Rightarrow Mg \times \dfrac{l}{2} \times \sin (30^\circ ) = mg \times \dfrac{l}{2} \times \sin (60^\circ )\]
From looking at the figure we have substituted the value of angle between the force and length.
 $M \times \dfrac{1}{2} = m \times \dfrac{{\sqrt 3 }}{2} $
 $ \Rightarrow \dfrac{M}{m} = \sqrt 3 $

Therefore the correct answer to the above question is (D) $\sqrt 3 $.

Note
If we make the free body diagram of the two rods then we will see that there is no other force acting on them except gravitational and hinge force so then obviously these two will balance each other out as the system in the figure is in equilibrium. As we considered the axis about which they rotate as the hinge hence while calculating the torque so the torque due to hinge force became zero.