Question

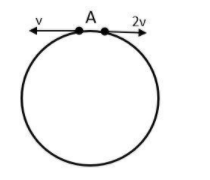
Two small particles of equal masses start moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are v and 2v respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at A, these two particles will again reach the point A?



a). 4
b). 3
c). 2
d). 1

Answer 1

Hint: It has been given that elastic collision will take place between the two particles and we know that in an elastic collision between two bodies, velocities are exchanged. A number of collisions will take place between the two particles before they both again reach at point A. We will have to first find the points on the circular path, where the collisions will take place. Then after we can find the number of collisions before the two particles meet each other.

Complete step by step answer:
Let us assume that the radius of the circular orbit be R and at time t = 0, the two particles start to move in opposite directions with velocity v and 2v.
Now, consider at time $t={t}_{1}$, the two particles again meet at some point B on the circumference of the orbit.
So, the distance travelled by both the particles will be $v{t}_{1}$ and $2v{t}_{1}$. And, both the particles will have to complete one complete revolution of the orbit together to meet again.
Thus, the distance travelled by both will be the perimeter of the orbit, that is $v{t}_{1}+2v{t}_{1}=2\pi R\implies {t}_{1}=\dfrac{2\pi R}{3v}$
Therefore, distance travelled by the two particles will be $\dfrac{2\pi R}{3}$ and $\dfrac{4\pi R}{3}$.
At point B, the two particles will exchange their velocities and will again meet at time $t=2{t}_{1}$ at point, say C after travelling distances $\dfrac{4\pi R}{3}$ and $\dfrac{2\pi R}{3}$.
We can represent the happenings as follows

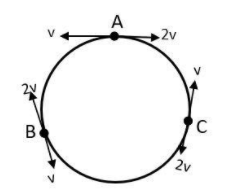
From the figure, the distance AB = BC = CA = $\dfrac{2\pi R}{3}$. The first collision took place at B and the second one at C.
After the second collision, both particles will have their initial velocities and initial travel direction. So, at time $t=3{t}_{1}$ they will travel the distances they have travelled in time ${t}_{1}$ and will reach point A again.
So, we can see that the two particles collided at points B and C.
Hence, option c is the correct answer.

Note: The direction and velocity of the particles after collisions take place should be kept in the mind or else wrong answers will come. In some questions, the particles can have unequal masses, so the velocities will not get exchanged directly and proportionate variations will happen.