Question

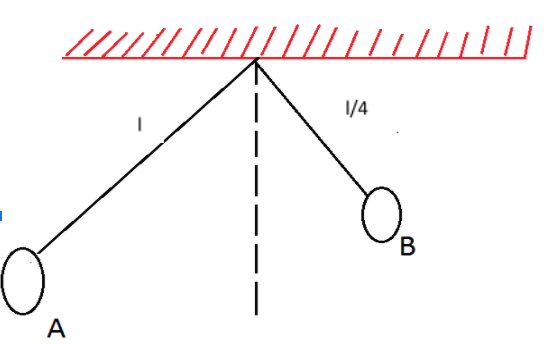
Two simple pendulums A and B having lengths $l$ and $\dfrac{l}{4}$ respectively, are released from the position as shown in figure. Calculate the time( in seconds) after which the two strings become parallel for the first time .
(Take $l = \dfrac{{90}}{{{\pi ^2}}}$ and $g = 10m/s^2$)(Both strings make equal angle with vertical initially)

Answer 1

Hint:$T = 2\pi \sqrt {\dfrac{l}{g}} $ (T is the time, l is the length of the pendulum string, g is the gravitational acceleration)
Angular position of the simple pendulum is given as:
$a\cos (\dfrac{{2\pi }}{T}t)$ (a is the amplitude, T is the time period and t is any time t)
Using above relations we will calculate the time period of the simple pendulums.

Complete step by step solution:
Let us define simple harmonic motion, Time period and we will discuss a simple pendulum.
Simple Harmonic motion: Simple Harmonic motion is the projection of uniform circular motion on a diameter of a circle of reference.
Time Period: It is the smallest interval of time at which the details of motion repeat.
Simple Pendulum: It is an idealized system consisting of an ideal, mass less and inelastic string whose one end is fixed to a support which is rigid and of infinite mass. A heavy point mass is suspended from the other end of the string.
Now, we will calculate the Time period.
We have two angles of the pendulum, one positive and the other is negative due to the clockwise and anticlockwise motion of the pendulum.
Therefore, we have
${\theta _1} = \theta \cos (\dfrac{{4\pi }}{T}t)$.............(1)
 ${\theta _2} = - \theta \cos (\dfrac{{2\pi }}{T}t)$$ = \theta \cos (\dfrac{{2\pi }}{T}t + \pi )$...........(2)
For the strings to be parallel for the first time, we will equate the equations 1 and 2
$ \Rightarrow \theta \cos (\dfrac{{4\pi }}{T}t) = \theta \cos (\dfrac{{2\pi }}{T}t + \pi )$
Using the calculation of cosine equations on both sides.
$ \Rightarrow \dfrac{{4\pi }}{T}t = 2n\pi \pm \left( {\dfrac{{2\pi }}{T}t + \pi } \right)$ (We have cancelled the common terms and removed the cosine term)
When n=0, $t = \dfrac{T}{2}$
When n=1, $t = \dfrac{T}{6}$
Therefore, time in seconds is given as :
$ \Rightarrow t = \dfrac{{2\pi }}{6}\sqrt {\dfrac{l}{g}}$
$ \Rightarrow t = \dfrac{\pi }{3}\sqrt {\dfrac{l}{g}}$
(We have divided the 6 by 2)
On substituting the values of $l$ and $g$
$ \Rightarrow t = \dfrac{\pi }{3}\sqrt {\dfrac{{90}}{{{\pi ^2}10}}} $
$ \Rightarrow t = \dfrac{\pi }{3}\sqrt {\dfrac{9}{{{\pi ^2}}}} $
$ \Rightarrow t = \dfrac{\pi }{3} \times \dfrac{3}{\pi } = 1$

Time is 1 second.

Note: Simple pendulums has many application like used in clocks for keeping time, used in metronome which helps maintain the speed of music, used in religious practices for burning incense sticks, for dowsing and divining purposes such as locating water, gold, oil and missing objects.