Question

Two positive charges value $ + Q$ are held in place and cannot move from the location shown below. A negative charge $q$ is only allowed to move along the $X$ axis and released from rest. Which of the following will happen?

(A) The charge $q$ will move in the direction of increasing $X$ values.
(B) The charge $q$ will not move.
(C) The charge $q$ will move in the direction of decreasing $X$ values.
(D) The charge $q$ will move with oscillatory motion.

Answer 1

Hint: Unlike charges exert an attractive electrostatic force on each other. The charge will move in the direction of the net force acting on it. Balancing the forces on the charge will give us the value of the net force and its direction.

Complete step by step answer:

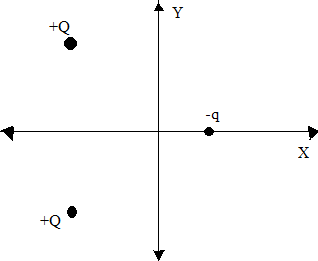
From the above figure we get to know that ${F_1}$ and ${F_2}$ are the two forces which are acting on the negative charge $ - q$ because of the positive charges $ + Q$. The force acting here is of electrostatic nature. So, electrostatic force can be calculated by the Coulomb’s Law, that is,
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
Where, $F = $electrostatic force
${q_1},{q_2} = $ Magnitudes of the charges
$r = $ Distance between the two charges.
$k = $ Proportionality constant $ = 9 \times {10^9}N{m^2}/{C^2}$
In this case,
$\Rightarrow {F_1} = \dfrac{{kQq}}{{{r^2}}}$
$\Rightarrow {F_2} = \dfrac{{kQq}}{{{r^2}}}$
$\Rightarrow {F_1} = {F_2} = F$
The formula for net force when both the forces are equal is,
$\Rightarrow {F_{net}} = 2F\cos \dfrac{\theta }{2}$
Now because of this force the negatively charged particle will start moving along the direction of decreasing $X$ values until the value of $\theta = {180^o}$ because at that point,
$\Rightarrow {F_{net}} = 2F\cos \dfrac{{180}}{2}$
$\Rightarrow {F_{net}} = 2F\cos 90$
$\Rightarrow {F_{net}} = 0$ because $\cos 90^\circ = 0$.
So at this point no net force is acting on the negatively charged particle. But it has attained velocity, because of which it will not stop moving. As soon as the particle starts moving a constantly varying net force again starts acting on it, which varies with the varying values of $\theta $ and will move until a position at which its velocity becomes zero and net force attains its maximum value. At that point the particle comes to rest momentarily and again starts moving but now in the opposite direction as compared to previous time. And this motion will go on continuously until any external force is applied on it. And this kind of motion is known as Oscillatory motion.

Hence option D is the correct answer.

Note: The position at which no net force is acting on the particle is known as mean position. The maximum displacement the particle can take from the mean position is known as its Amplitude. When the particle starts from the mean position goes towards the positive extreme, returns to the mean position goes to the negative extreme and again comes back to the mean position, this complete cycle is known as one oscillation.