Question

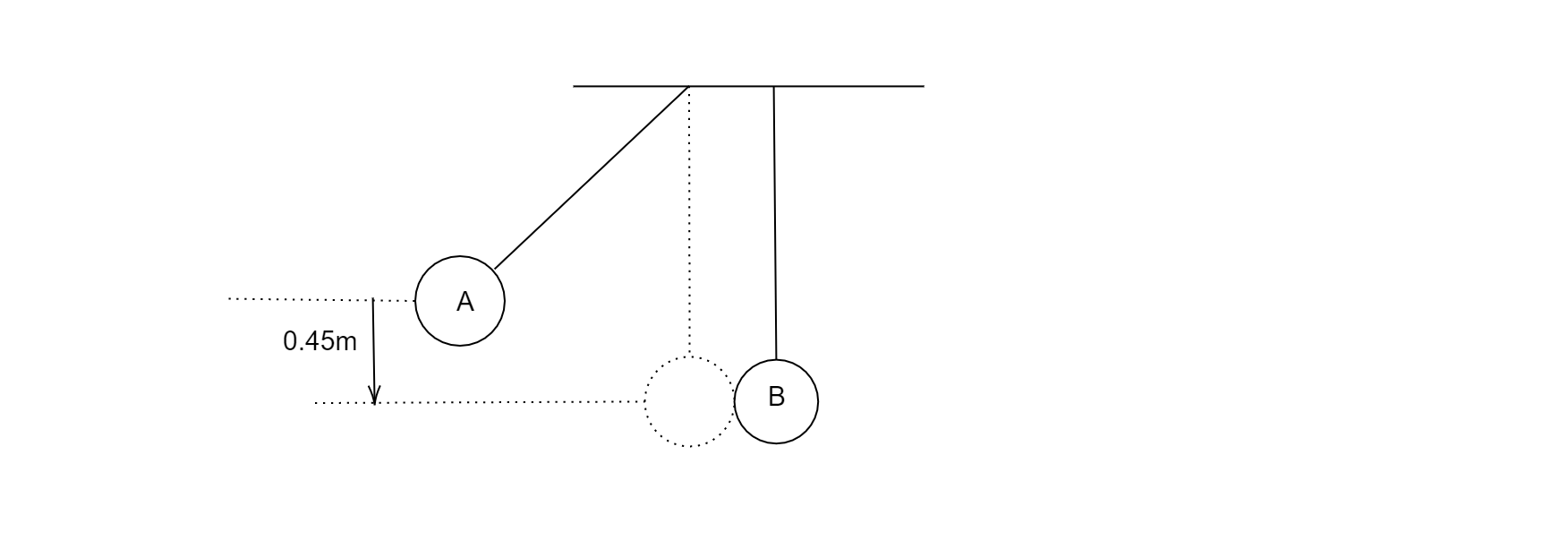
Two massless strings of length $5m$ hang from the ceiling very near to each other, as shown in the figure. Two balls $A$ and $B$ of masses $0.25kg$ and $0.5kg$ are attached to the string. The ball $A$ is released from rest at a height $0.45m$, as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of the ball $B$ is $1J$. The velocity of the ball $A$, just after the collision is
A) $5m{s^{ - 1}}$ to the right
B) $5m{s^{ - 1}}$ to the left
C) $1m{s^{ - 1}}$ to the right
D) $1m{s^{ - 1}}$ to the left

Answer 1

Hint: The law of conservation of momentum states that the two objects’ total momentum before and after the collision is conserved in an isolated system. This property of momentum conservation during a collision can be used to find out the velocity of the ball $A$ after the collision.

Complete step by step solution:
As given in the question:
${m_A} = 0.25kg$
${m_B} = 0.5kg$
$h = 0.45m$
The velocity of the ball $A$ just before the collision can be calculated by the conservation of energy we get:
${m_A}gh = \dfrac{1}{2}{m_A}{({v_A})^2}$
Where ${m_A}$ is the mass of the ball $A$
${v_A}$ is the velocity of the ball $A$ before the collision
$g$ is the acceleration due to gravity
$h$ is the initial height of the ball $A$
Therefore, ${v_A} = \sqrt {2gh}$
$\Rightarrow {v_A} = \sqrt {2 \times 9.8 \times 0.45} = 3m/s$
After the collision, let the velocity of the ball $B$ be ${v_B}$ after the collision by the conservation of energy we get:
$\Rightarrow {E_B} = \dfrac{1}{2}{m_B}{({v_B})^2}$
Where ${m_B}$ is the mass of the ball $B$
${v_B}$ is the velocity of the ball $B$ after the collision
${E_B}$ is the energy of the ball $B$
On putting ${E_B} = 1J$, we get:
$\Rightarrow {v_B} = \sqrt {\dfrac{{2 \times 1}}{{0.5}}} = 2m/s$
The elastic momentum is conserved in a collision, therefore:
The momentum of the ball $A$ before collision = Momentum of the balls after collision
$\Rightarrow {m_A}{v_{Ai}} = {m_A}{v_A} + {m_B}{v_B}$
$\Rightarrow 0.25 \times 3 = 0.25 \times {v_A} + 0.5 \times 2$
$\Rightarrow 0.75 = 0.25{v_A} + 1$
$\Rightarrow {v_A} = - 1m/s$, all the velocities were considered to be in the right direction since ${v_A}$ is negative; therefore, it might be in the opposite direction, i.e., to the right.
Therefore, the velocity of the ball $A$ just after the collision will be $1m{s^{ - 1}}$ to the left.

The correct answer is option (D).

Note: The momentum conservation should be used only when the mass of the objects remains constant during the collision, which means the collision should also follow mass conservation, or we can say that the system must be an isolated system.