Question

Two identical uniform discs of mass m and radius r are arranged as shown in the figure. If \[\alpha \] is the angular acceleration of the lower disc and ​is the acceleration of the center of mass of the lower disc, then find the relation among \[{a_{cm}}\]​, \[\alpha \] and r.


A. \[{a_{cm}} = \dfrac{\alpha }{r}\]
B. \[{a_{cm}} = 2\alpha r\]
C. \[{a_{cm}} = \alpha r\]
D. None of these

Answer 1

Hint:Before we start addressing the problem, we need to know about what data has been provided and what we need to solve. Here they have given the mass of two identical discs as m and r , the angular acceleration of the lower disc is \[\alpha \] and the acceleration of the center of mass of the lower disc is \[{a_{cm}}\], then we need to find the relation among \[{a_{cm}}\]​, \[\alpha \] and r.

Complete step by step solution:

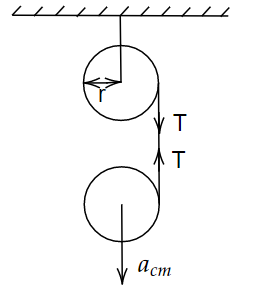
Image: Two identical uniform discs.

As shown in figure the tension T is acting on the discs having radius r
If we apply torque for the above disc at the centre then,
\[\tau = I \times \alpha \]
\[T \times r = \dfrac{{m{r^2}}}{2} \times {\alpha _1}\]
\[{\alpha _1} = \dfrac{{2T}}{{mr}}\]…… (1)
Now, if we apply the torque to the lower disc we get,
\[T \times r = \dfrac{{m{r^2}}}{2} \times \alpha \]
\[\alpha = \dfrac{{2T}}{{mr}}\]……….. (2)
From equation (1) and (2) we will have,
 \[{\alpha _1} = \alpha \]….. (1)

Since the centre of mass of the lower disc passes through its centre then the centre of mass will become zero. Then, the acceleration of the above disc = Acceleration of the below disc
\[r{\alpha _1} = {a_{cm}} - r\alpha \]
Substitute the value \[{\alpha _1} = \alpha \] in above equation we get,
\[{a_{cm}} = 2r\alpha \]
Therefore, then the relation among \[{a_{cm}}\]​, \[\alpha \] and r is \[{a_{cm}} = 2r\alpha \].

Hence, option B is the correct answer.

Note: Here, in this problem it is important to remember that, the definition of angular acceleration, and also when the two identical uniform discs of mass m and radius r are connected through a string as shown we need to identify in which direction the torque will be acting.