Question

Two equal bar magnets are kept as shown in the figure. The direction of resultant magnetic field, indicated by arrow head at the point P is (approximately)


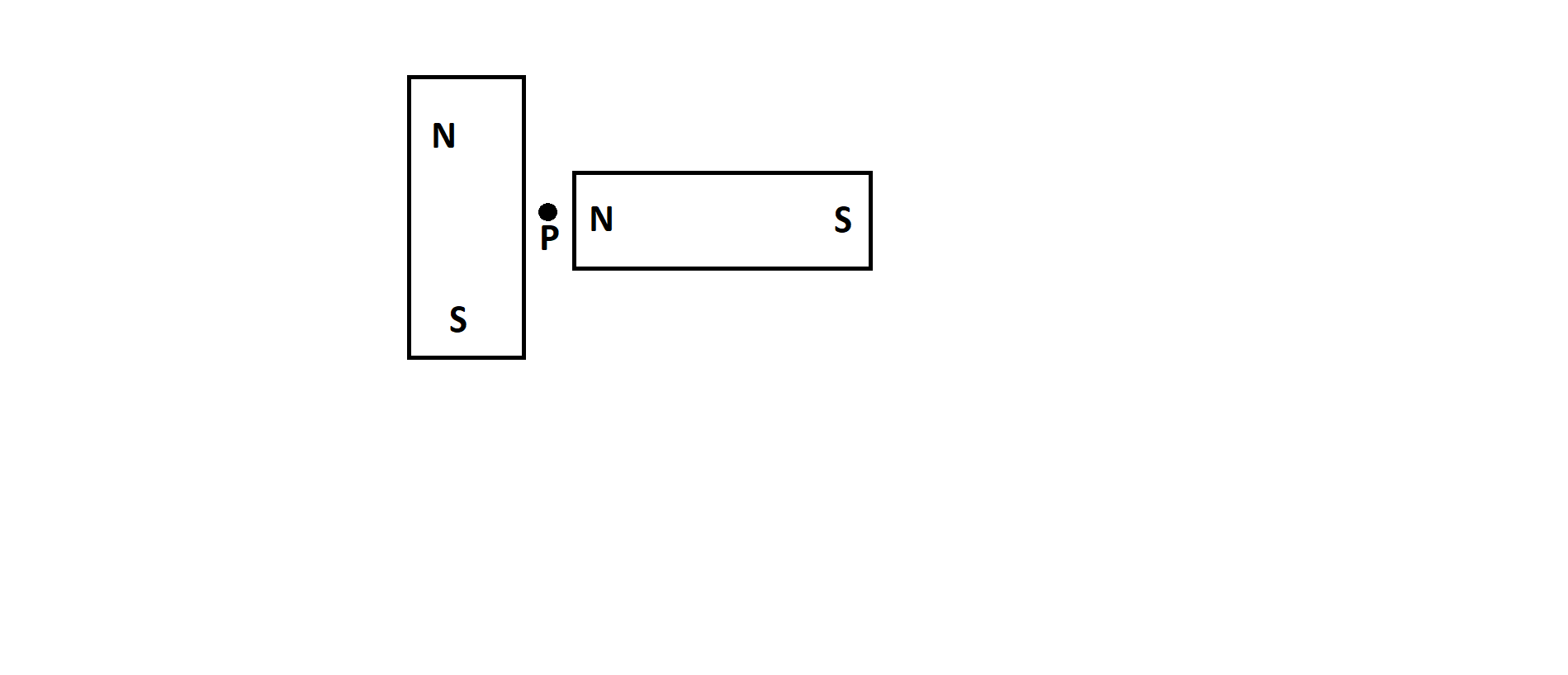
a) $ \to $
b) $ \nearrow $
c) $ \searrow $
d) $ \uparrow $

Answer 1

Hint:
Magnetic field is actually a vector quantity. For this reason we cannot just add them based on their magnitude to get the resultant magnetic field when they are perpendicular to each other. Therefore we can determine the direction of the net magnetic field of them by using resultant vector addition.




Complete step by step solution:
We know that vector quantities have both direction and magnitude. Same characteristics are found for magnetic fields, as they have both the direction as well as magnitude at a particular point. Magnetic field also follows the vector cross product rule. Hence the magnetic field is a vector quantity.
Even if there is another magnetic field present , the resultant of two magnetic fields would also follow the rules of vector addition.
Here in the given question, two equal bar magnets are placed perpendicular to each other. Hence, these two magnets produce magnetic fields around them. The direction of the resultant magnetic field can be determined by drawing a tangent to the magnetic lines of force.
Here the magnetic force of lines points to the region in which the magnetic force can be detected. Therefore the magnetic force of lines is nothing but a region of magnetic field.
So now we can draw magnetic field lines on that point for two magnets.

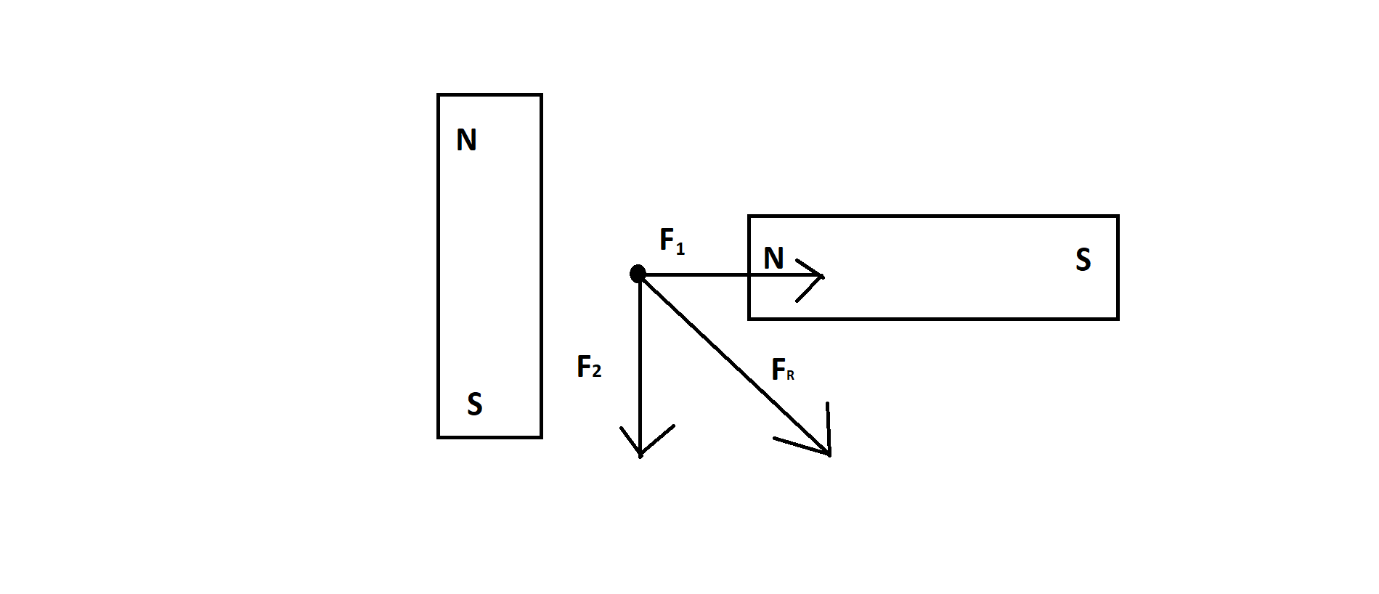
Now here we draw an image of the line of force at point P due to bar magnets. Here we see that the magnetic line of force ${F_1}$ is horizontal and ${F_2}$ is in vertical direction. Now if we find the resultant of these two vectors, we get ${F_R}$ . Now if we compare the option with them then we $ \searrow $ is the approximately matching with ${F_R}$ .





Therefore, the correct option is C.



Note:
 The two magnetic field lines do not cross each other and there is a specific reason behind it. If two magnetic fields of lines would intersect then there would be two directions of the magnetic field at a certain point of time. This is just impossible.