Question

Two blocks of mass $m = 5Kg$ and $M = 10Kg$ are connected by a string passing over a pulley B as shown. Another string connects the center of pulley B to the floor and passes over another pulley A as shown. An upward force F is applied at the center of pulley A. Both the pulleys are massless. An upward force F is applied in the pulley A. Find the acceleration of blocks m and M if F is $100N$.

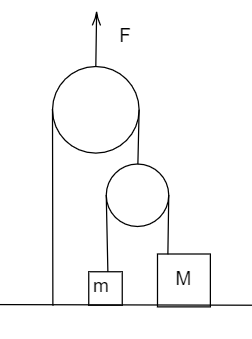
(A)$0\dfrac{m}{{{s^2}}};0\dfrac{m}{{{s^2}}}$
(B)$5\dfrac{m}{{{s^2}}};2.5\dfrac{m}{{{s^2}}}$
(C)$10\dfrac{m}{{{s^2}}};5\dfrac{m}{{{s^2}}}$
(D)$2.5\dfrac{m}{{{s^2}}};5\dfrac{m}{{{s^2}}}$

Answer 1

Hint For lifting a body in an upward direction the upward directing force must be greater than the force acting in the downward direction. Tension in a massless string is the same along its length. We will use this property to solve this question.

Complete Step-by-step solution
Let,
${T_0}$​= tension in the string passing over A
${T_1}$= tension in the string passing over B
Free body diagram:

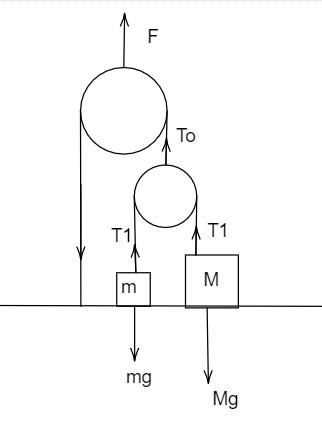
$\therefore 2{T_0}= F$ and $2{T_1} = {T_0}$(balancing forces in the free body diagram drawn above)
$ \Rightarrow {T_1} = \dfrac{F}{4}$ (It’s given in the question that $F=100N$)
$ \therefore {T_1} = 25N$
The upward force on block m and M is the same as that force is due to tension in the string which is the same across its length as tension in a massless string is the same along its length.
Weights of blocks are,
$M=10Kg$ and $m=5Kg$ (given in question)
$mg = 50N$ and $Mg = 100N$ (Weight is the downward force acting on the block)
As${T_1}$ is less than mg and Mg hence the blocks will remain stationary on the floor as for lifting a body in an upward direction the upward directing force must be greater than the force acting in the downward direction. So, the acceleration of both the blocks will be zero as they are at rest.

$\therefore $ Hence, the correct answer will be (A)$0\dfrac{m}{{{s^2}}};0\dfrac{m}{{{s^2}}}$.

Note As discussed earlier tension along the same massless string will be the same this is an important point to be noted as many students consider tension in both strings different and end up making mistakes due to this mistake there time also got wasted in the examination hall and could get negative marks in the question.