Question

To measure the potential difference across the resistor of resistance R a voltmeter with resistance ${R_v}$ is used. To measure the potential with minimum accuracy of 95% then
(A) ${R_v} = 5R$
(B) ${R_v} = 15R$
(C) ${R_v} = 10R$
(D) ${R_v} > 19R$

Answer 1

Hint At first, calculate the voltage for the resistance $R$ and then, calculate the voltage reading for the voltmeter of equivalent resistance. Then, by using the expressions for voltage for $R$ and equivalent resistance for voltmeter for the 95% accuracy.

Complete Step by Step Solution


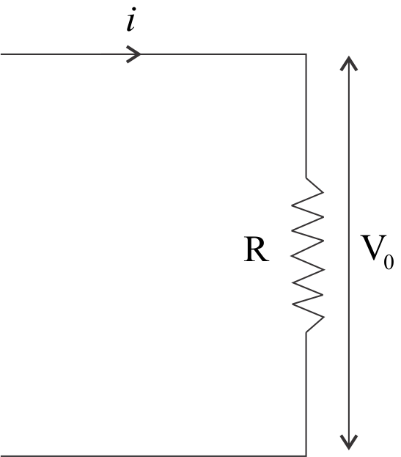
In the above figure, we have to use the Ohm’s law which states that the current through the conductor between two points is directly proportional to the voltage across the two points. So, by using the ohm’s law we can find the value for ${V_0}$ as –
${V_0} = ir \cdots \left( 1 \right)$
Now, drawing the figure with the voltmeter of resistance ${R_v}$ -


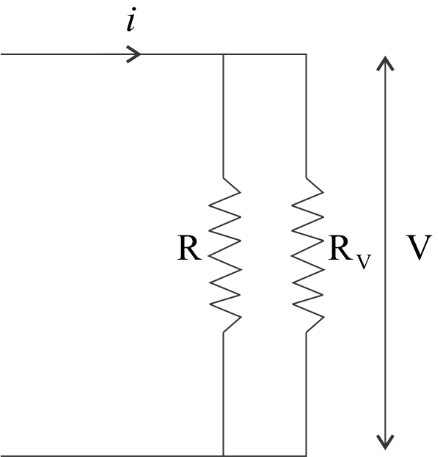
Now, finding the equivalent resistance in the above figure –
From the above figure, we can see that the resistances $R$ and ${R_v}$ are parallel to each other. So, -
$
   \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{R} + \dfrac{1}{{{R_v}}} \\
   \Rightarrow {R_{eq}} = \dfrac{{R{R_v}}}{{R + {R_v}}} \\
 $
Again, using the ohm’s law, finding the expression for voltage –
$V = i\dfrac{{R{R_v}}}{{R + {R_v}}} \cdots \left( 2 \right)$
Now, according to the question, it is given that, accuracy should be 95% then, we get –
$ \Rightarrow V = 0.95{V_0}$
Using the value of $V$ and ${V_0}$ from equation (1) and equation (2), we get –
$ \Rightarrow i\dfrac{{R{R_v}}}{{R + {R_v}}} = 0.95\left( {iR} \right)$
By further solving, we get –
$
   \Rightarrow {R_v} > 0.95R + 0.95{R_v} \\
   \Rightarrow 0.05{R_v} > 0.95R \\
   \Rightarrow {R_v} > \dfrac{{0.95}}{{0.05}}R \\
  \therefore {R_v} > 19R \\
 $

Hence, from the above expression we can see that option (D) is the correct answer.

Note As the accuracy should be 95% so, it can be rewritten as $\dfrac{{95}}{{100}}$ after solving this we get the efficiency as 0.95 which is to be used during the solving of the problem.