Question

There is a uniform spherically symmetric surface charge density at a distance ${R_0}$ from the origin. The charge distribution is initially at rest and starts expanding because of mutual repulsion. The figure that represents best the speed $V(R(t))$ of the distribution as a function of its instantaneous radius $R(t)$ is
(A)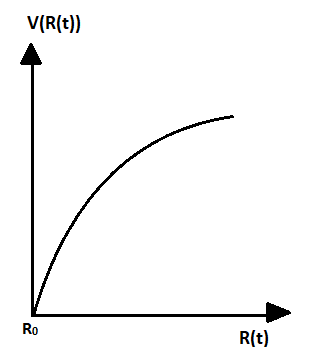






(B)

(C)







(D)

Answer 1

Hint: Keep in mind that there is no external force applied. Therefore, the work done by the external force is also zero. In this question, you have to apply the work-energy theorem. So recall all concepts of the work-energy theorem.

Complete step by step answer:
Let us assume a uniform spherically symmetric surface charge density with radius R₀. The charge distribution is initially at rest as shown in figure

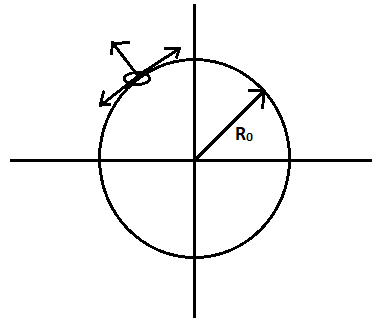
and also assume there is a charged particle that experiences a force shown in figure above, due to this figure the sphere starts expanding and becomes like shown in figure below.


As there is no external force applied. Therefore, the work done by the external force is also zero.
${F_{ext}} = 0$
$ \Rightarrow {W_{ext}} = 0$
Now, applying work energy theorem,
According to the work energy theorem, work done by all forces is equal to change in kinetic energy.
${W_{all}} = \Delta K$
$ \Rightarrow {W_E} + {W_g} + {W_{ext}} = \Delta K$
Here, ${W_g} = 0$, as no work done by the gravitational force
And ${W_E}$ is the work done by the electric field and it is a central force that is conservative in nature.
$ \Rightarrow - \Delta U = \Delta K$
$ \Rightarrow - ({U_f} - {U_i}) = {K_f} - {K_i}$
On further solving, we get
$ \Rightarrow {U_i} + {K_i} = {U_i} + {K_f}$
We now that work done by electric field is given by,
$U = \dfrac{{k{Q_1}{Q_2}}}{{2R}}$
So, on putting the value in the above equation, we get
\[ \Rightarrow \dfrac{{k{Q^2}}}{{2{R_0}}} + 0 = \dfrac{{k{Q^2}}}{{2R}} + \dfrac{1}{2}m{v^2}\]
$ \Rightarrow m{v^2} = k{Q^2}\left( {\dfrac{1}{{{R_0}}} - \dfrac{1}{R}} \right)$
On further solving, we get
$ \Rightarrow v = \sqrt {\left( {\dfrac{{k{Q^2}}}{m}} \right)\left( {\dfrac{1}{{{R_0}}} - \dfrac{1}{R}} \right)} $
On differentiating the above term with respect to R, we get
$\dfrac{{dv}}{{dR}} = \left( {\dfrac{{k{Q^2}}}{m}} \right)\left( {\dfrac{1}{{{R^2}}}} \right)\dfrac{1}{{2v}}$
Here in the above equation all the terms are positive. So we can drive from that $\dfrac{{dv}}{{dR}}$ is also positive and decreasing with an increase in $R$.
And the slope of the V-R curve is decreasing.
Therefore, the correct answer is an option (A)

Note: The work-energy theorem can be derived from Newton’s second law. The work-energy theorem is another example of the conservation of energy. A force only does work on an object for the time that it is in contact with the object.