
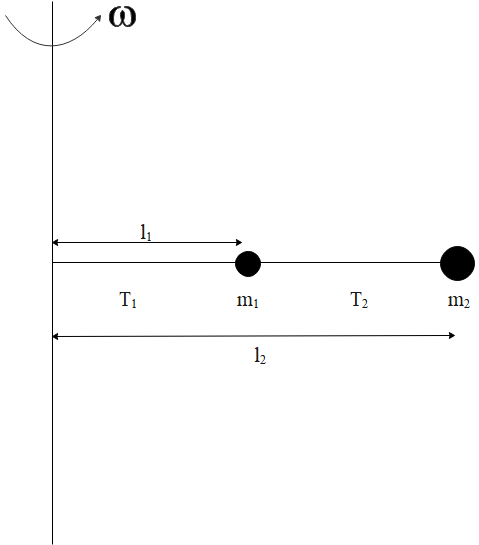
The whole set up shown in the figure is rotating with constant angular velocity $\omega $ on a horizontal frictionless table then the ratio of tensions $\dfrac{{{T_1}}}{{{T_2}}}$ is (Given $\dfrac{{{l_1}}}{{{l_2}}} = \dfrac{2}{1}$)
(A) $\dfrac{{{m_1}}}{{{m_2}}}$
(B) $\dfrac{{({m_1} + 2{m_g})}}{{2{m_2}}}$
(C) $\dfrac{{{m_2}}}{{{m_1}}}$
(D) $\dfrac{{({m_2} + {m_1})}}{{{m_2}}}$
Answer
217.8k+ views
Hint: To answer this question we have to find the expression of ${T_1}$ and ${T_2}$. Once we have the expressions we have to find the ratio of $\dfrac{{{T_1}}}{{{T_2}}}$, and put the values of the expressions. After evaluating the expressions, we will have the answer to the required question.
Complete step by step answer:
First we need to find the value of ${T_2}$. So the value of ${T_2}$is as follows:
${T_2} = {m_2}{w^2}{l_2}$
Now we have to find the value of ${T_1}$. So the value of ${T_1}$is as follows:
${T_1} = {m_2}{w^2}{l_2} + {m_2}{w^2}{l_1}$
We know that we have to find the value of the ratio between ${T_1}$ and ${T_2}$. So here is the ratio between them:
$T = mg$$\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{{m_2}{w^2}{l_1} + {m_2}{w^2}{l_2}}}{{{m_2}{w^2}{l_2}}}$
After the ratio is evaluated then we can get the expression as:
$\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{[{m_1} + {m_2}\dfrac{{{l_2}}}{{{l_1}}}]{l_2}}}{{{m_2}{l_2}}} = \dfrac{{({m_1} + 2{m_2})}}{{2{m_2}}}$
Hence we can say that the $\dfrac{{{T_1}}}{{{T_2}}}$is $\dfrac{{({m_1} + 2{m_g})}}{{2{m_2}}}$.
So the correct answer is option B.
Note: We should be aware of the meaning of angular velocity. By definition, angular velocity signifies how much fast a body can rotate or revolve relative to that of the other body point. This means how fasts the angular position of the orientation of a body will vary with the time.
We should also be knowing the definition of the term tension for better understanding. By tension we mean that it is the pulling force that is transmitted axially from a cable, which is usually a one dimensional body, or even by each end from a three dimensional body. Tension is formulated as being similar to the mass of the object multiplied with the gravitational force, also described as the subtraction or addition of the mass multiplied by acceleration.
The formula of tension is given as:
$T = mg$.
Complete step by step answer:
First we need to find the value of ${T_2}$. So the value of ${T_2}$is as follows:
${T_2} = {m_2}{w^2}{l_2}$
Now we have to find the value of ${T_1}$. So the value of ${T_1}$is as follows:
${T_1} = {m_2}{w^2}{l_2} + {m_2}{w^2}{l_1}$
We know that we have to find the value of the ratio between ${T_1}$ and ${T_2}$. So here is the ratio between them:
$T = mg$$\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{{m_2}{w^2}{l_1} + {m_2}{w^2}{l_2}}}{{{m_2}{w^2}{l_2}}}$
After the ratio is evaluated then we can get the expression as:
$\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{[{m_1} + {m_2}\dfrac{{{l_2}}}{{{l_1}}}]{l_2}}}{{{m_2}{l_2}}} = \dfrac{{({m_1} + 2{m_2})}}{{2{m_2}}}$
Hence we can say that the $\dfrac{{{T_1}}}{{{T_2}}}$is $\dfrac{{({m_1} + 2{m_g})}}{{2{m_2}}}$.
So the correct answer is option B.
Note: We should be aware of the meaning of angular velocity. By definition, angular velocity signifies how much fast a body can rotate or revolve relative to that of the other body point. This means how fasts the angular position of the orientation of a body will vary with the time.
We should also be knowing the definition of the term tension for better understanding. By tension we mean that it is the pulling force that is transmitted axially from a cable, which is usually a one dimensional body, or even by each end from a three dimensional body. Tension is formulated as being similar to the mass of the object multiplied with the gravitational force, also described as the subtraction or addition of the mass multiplied by acceleration.
The formula of tension is given as:
$T = mg$.
Recently Updated Pages
Elastic Collision in Two Dimensions Explained Simply

Elastic Collisions in One Dimension Explained

Electric Field Due to a Uniformly Charged Ring Explained

Electric Field of Infinite Line Charge and Cylinders Explained

Electric Flux and Area Vector Explained Simply

Electric Field of a Charged Spherical Shell Explained

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Understanding Atomic Structure for Beginners




