Question

The velocity of current in a river grows in proportion to the distance from its bank and reaches the maximum value $v_0$ in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. If the distance through which the boat crosses the river is carried away by the current, $\dfrac{{bc{v_0}}}{{2u}}$, where c is the width of the river. Find b.

Answer 1

Hint: When the boat travels in the direction perpendicular (say y-direction) to that of the flow of the river the river current will also push the boat in its own direction(say x-direction). Which means that the final velocity of the boat will be the resultant of its own velocity in y-direction and the velocity of river current in x-direction.

Complete step by step answer:



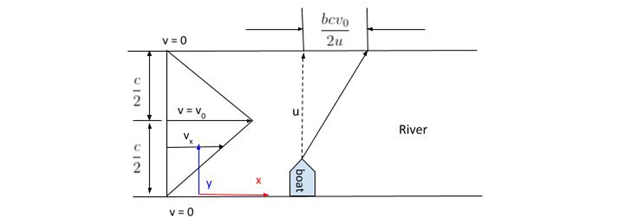
The speed of the boat is u m/s, speed of the river stream rises proportional to its distance from the bank and is maximum at the centre of the river and it has a value of $v_0$ m/s.
Velocity of the boat in y-direction (i.e. perpendicular to the flow),
${v_y} = \dfrac{{dy}}{{dt}}$
$\dfrac{{dy}}{{dt}} = u$...................(1)
Velocity of the boat in x-direction (i.e. along the flow of stream), consider the stream at a distance y from the bank having velocity $v_x$. By similarity of triangles we can say,
$\dfrac{{{v_x}}}{y} = \dfrac{{{v_0}}}{{\left( {c/2} \right)}} \Rightarrow {v_x} = \dfrac{{2{v_0}}}{{cy}}$
${v_x} = \dfrac{{dx}}{{dt}} \Rightarrow \dfrac{{dx}}{{dt}} = \dfrac{{2{v_0}}}{{cy}}$.................(2)
Divide equation (1) by equation (2) we get,
$\dfrac{{dy}}{{dx}} = \dfrac{{uc}}{{2{v_0}y}}$
Rearranging and integrating above equation,
$\int\limits_0^y {ydy = } \dfrac{{uc}}{{2{v_0}}}\int\limits_0^x {dx} $
${y^2} = \dfrac{{ucx}}{{{v_0}}}$................ (3)
Putting $y = \dfrac{c}{2}$in the above equation we get,
$x = \dfrac{{c{v_0}}}{{4u}}$
Also, for the total distance travelled in x-direction $x_{net}$ is given by,
${x_{net}} = 2x \Rightarrow {x_{net}} = \dfrac{{c{v_0}}}{{2u}}$..................(4)
But total distance travelled in x-direction due to the river current is given in the problem as,
${x_{net}} = \dfrac{{bc{v_0}}}{{2u}}$..................(5)

Comparing equations (4) & (5) we get, $b = 1$.

Note: The triangle shown in the figure signifies the linear variation of the velocity of river current with respect to its distance from the banks of the river. So at any arbitrary distance y we can calculate the velocity of the river current, by using the equation ${v_x} = \dfrac{{2{v_0}}}{{cy}}$ which was derived by applying the concept of similarity of triangles.