Question

The vectors of magnitude a, 2a, and 3a meet at a point and their directions are along the diagonals of three adjacent faces of a cube. Determine the magnitude of their resultant.
A. 5a
B. 6a
C. 10a
D. 9a

Answer 1

Hint: In this question, we need to find the magnitude of the resultant of three vectors. For this, we need to assume that all the sides of a cube are of unit length and also unit vectors along with OA, OB and OC are \[\hat i,\hat j,\hat k\]respectively. For finding the magnitude of the resultant vector, we will use the following formula.

Formula used:
The resultant of the vector \[a\hat i + b\hat j + c\hat k\] is given by \[\sqrt {{a^2} + {b^2} + {c^2}} \].

Complete step by step solution:
Let us assume that every side of a cube is of unit length. Also, the unit vectors along with OA, OB, and OC are \[\hat i,\hat j,\hat k\] respectively.Consider the following figure.



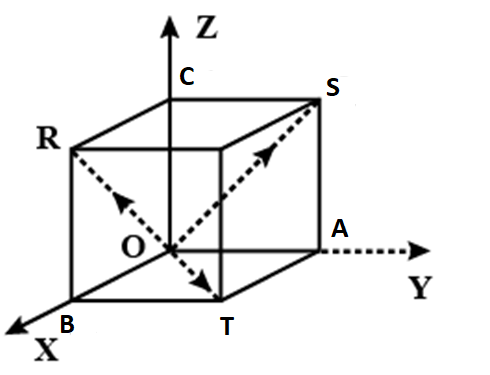
Here, we can say that OR, OS, and OT are the diagonals of a cube having respective magnitudes of vectors a, 2a, and 3a respectively.
So, the vector along OR is \[a\left( {\dfrac{{\hat j + \hat k}}{{\sqrt 2 }}} \right)\]
The vector along OS is \[2a\left( {\dfrac{{\hat k + \hat i}}{{\sqrt 2 }}} \right)\]
And the vector along OT is \[3a\left( {\dfrac{{\hat i + \hat j}}{{\sqrt 2 }}} \right)\]
Thus, the resultant vector R is the addition of all three vectors such as vector OR, vector OS and the vector OT.
Hence, \[R = a\left( {\dfrac{{\hat j + \hat k}}{{\sqrt 2 }}} \right) + 2a\left( {\dfrac{{\hat k + \hat i}}{{\sqrt 2 }}} \right) + 3a\left( {\dfrac{{\hat i + \hat j}}{{\sqrt 2 }}} \right)\]
By simplifying, we get
\[R = \dfrac{{a\hat j + a\hat k}}{{\sqrt 2 }} + \dfrac{{2a\hat k + 2a\hat i}}{{\sqrt 2 }} + \dfrac{{3a\hat i + 3a\hat j}}{{\sqrt 2 }}\]
\[\Rightarrow R = \dfrac{{a\hat j + a\hat k + 2a\hat k + 2a\hat i + 3a\hat i + 3a\hat j}}{{\sqrt 2 }}\]
\[\Rightarrow R = \dfrac{{2a\hat i + 3a\hat i + 3a\hat j + a\hat j + a\hat k + 2a\hat k}}{{\sqrt 2 }}\]
By simplifying further, we get
\[R = \dfrac{{5a\hat i + 4a\hat j + 3a\hat k}}{{\sqrt 2 }}\]
Let us separate the denominators.
Thus, we get
\[R = \dfrac{{5a}}{{\sqrt 2 }}\hat i + \dfrac{{4a}}{{\sqrt 2 }}\hat j + \dfrac{{3a}}{{\sqrt 2 }}\hat k\]
Let us find the magnitude of the resultant R .
\[\left| R \right| = \sqrt {{{\left( {\dfrac{{5a}}{{\sqrt 2 }}} \right)}^2} + {{\left( {\dfrac{{4a}}{{\sqrt 2 }}} \right)}^2} + {{\left( {\dfrac{{3a}}{{\sqrt 2 }}} \right)}^2}} \]
\[\Rightarrow \left| R \right| = \sqrt {\left( {\dfrac{{25{a^2}}}{2}} \right) + \left( {\dfrac{{16{a^2}}}{2}} \right) + \left( {\dfrac{{9{a^2}}}{2}} \right)} \]
\[\Rightarrow \left| R \right| = \sqrt {\left( {\dfrac{{25{a^2} + 16{a^2} + 9{a^2}}}{2}} \right)} \]
By simplifying further, we get
\[\left| R \right| = \sqrt {\left( {\dfrac{{50{a^2}}}{2}} \right)} \]
\[\Rightarrow \left| R \right| = \sqrt {25{a^2}} \]
\[\therefore \left| R \right| = 5a\]
Hence, the magnitude of the resultant vector is 5a.

Therefore, the correct option is (A).

Note: Here, students generally make mistakes in finding the resultant vector. If so, then its magnitude will be wrong. Also, the simplification part is also valuable here.