Question

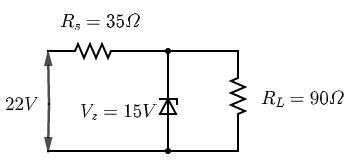
The value of power dissipated across the Zener diode (${V_Z} = 15V$) connected in the circuit as shown in the figure is $x \times {10^{ - 1}}$ watt. What is the value of x?

Answer 1

Hint: We will first draw the circuit with the current showing in each branch and then solve for the current flowing through the Zener diode branch, and then using the general formula of power dissipation we will find the power dissipated at Zener diode and then we will find the exact value of x.

Formula Used:
If V is the voltage and I is the current flowing through a part of the circuit then power dissipated is given by $P = VI$

Complete answer:
Let us draw the circuit with current $i$ flowing from $22V$ battery and ${i_2}$ through the Zener diode and ${i_1}$ through the ${R_L} = 90\Omega $ also, voltage across ${R_S}$ will be $22 - 15 = 7V$ as shown in circuit

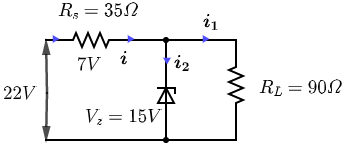
Now, Current $i$ can simply be calculated as
$
  i = \dfrac{7}{{{R_S}}} \\
  i = \dfrac{7}{{35}} \\
  i = \dfrac{1}{5}A \\
 $

and, ${i_1}$ can simply be calculated as
$
  {i_1} = \dfrac{{15}}{{{R_L}}} \\
  {i_1} = \dfrac{{15}}{{90}} \\
  {i_1} = \dfrac{1}{6}A \\
 $

Now, for total current we can see from the circuit that,
${i_2} = i - {i_1}$ on putting the values we get,
$
  {i_2} = \dfrac{1}{5} - \dfrac{1}{6} \\
  {i_2} = \dfrac{1}{{30}}A \\
 $

Now, voltage across the zener diode is $15V$${i_2} = \dfrac{1}{{30}}A$ then, power dissipation is given by the formula $P = VI$ on putting the values we get
$
  P = 15 \times \dfrac{1}{{30}} \\
  P = 0.5 \\
   \Rightarrow P = 5 \times {10^{ - 1}}W \\
 $
so, on comparing this value of power with given expression as $x \times {10^{ - 1}}$
we get, $x = 5$

Hence, the value of $x$ is $5$.

Note: The general relation between resistance, voltage, and current is given by ohm’s law where resistance is equal to the ratio of voltage and current, and always draw the circuit diagram with the current direction and its breakdown at junctions to solve such kind of questions easily.