Question

The rolling object rolls without slipping down an incline plane (angle of inclination \[\theta \]), then the minimum acceleration it can have is:
(A) \[g\sin \theta \]
(B) \[\dfrac{{2g\sin \theta }}{3}\]
(C) \[\dfrac{{g\sin \theta }}{2}\]
(D) zero

Answer 1

Hint: We will first apply Newton’s laws of motion to calculate acceleration on an inclined plane for pure rolling. We can also directly use the formula for acceleration: -
 \[a = \dfrac{{g\sin \theta }}{{1 + \dfrac{I}{{m{R^2}}}}}\]
Where,
a = acceleration of the rolling body on the incline. (pure rolling)
  \[\theta \] = inclination of the plane from horizontal.
g = acceleration due to gravity.
I = moment of inertia of the body about its centre of mass.
R = radius of the rolling body.
After calculating this acceleration, we will check for its minimum possible value.

Complete step by step solution

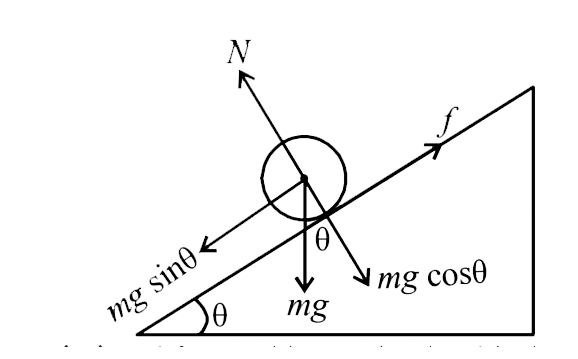
Figure 1/Pure Rolling on an inclined Plane
We will apply Newton’s Law of motion along the incline: -
 \[\sum F = m\overrightarrow a \]
Where,
 \[\sum F = \] Net Force acting on the body.
M = mass of the body.
a = acceleration of the body in the direction of force.
 \[mg\sin \theta - f = ma\] . . . (1)
We will apply newton’s Law for rotational mechanics: -
 \[\sum \tau = I\alpha \]
Where,
 \[\sum \tau \] = Net Torque acting on the body.
I = Inertia of the body about centre of mass.
 \[\alpha \] = Angular Acceleration of the body.
 \[f \times R = I \times \dfrac{a}{R}\] (using \[a = \alpha R\] )
 \[f = \dfrac{{Ia}}{{{R^2}}}\] . . . (2)
Adding (1) and (2) we get: -
 \[mg\sin \theta = ma + \dfrac{{Ia}}{{{R^2}}}\]
 \[g\sin \theta = a + \dfrac{{Ia}}{{m{R^2}}}\]
 \[g\sin \theta = a(1 + \dfrac{I}{{m{R^2}}})\]
 \[ \Rightarrow a = \dfrac{{g\sin \theta }}{{1 + \dfrac{I}{{m{R^2}}}}}\]
Now, in the above formula we see that acceleration will be minimum when the denominator = \[1 + \dfrac{I}{{m{R^2}}}\] will be maximum. The denominator will be maximum for the maximum value of I.
I have its maximum possible value for a ring which is ‘mR$^2$’. Thus, we take \[I = m{R^2}\] .
Now, acceleration becomes: -
 \[a = \dfrac{{g\sin \theta }}{{1 + \dfrac{{m{R^2}}}{{m{R^2}}}}}\]
 \[a = \dfrac{{g\sin \theta }}{{1 + 1}}\]
 \[ \Rightarrow a = \dfrac{{g\sin \theta }}{2}\]

Hence, option(c) is correct.

Note
(A) In the above question, it is stated that the object rolls without slipping. This is the case for pure rolling. Hence, frictional force will be self-adjusting and not equal to maximum value of friction, that is, \[{\mu _s}N\] . Thus, do not keep f = \[{\mu _s}N\] in the above question to calculate acceleration using eq-(1).
(B) However, this is exactly what is done to calculate acceleration when the rolling motion is not pure. In that case, acceleration is given by the following equation: -
 \[a = g\sin \theta - {\mu _k}\cos \theta \] (for impure rolling motion)
(C) Also, remember that the relation: - “ \[a = \alpha R\] ” is only valid in case of pure rolling motion and that is why we were able to use this relation in the above question.