Question

The reason for the change in shape of a regular body is

(A) Volume stress
(B) Shearing strain
(C) Longitudinal strain
(D) Metallic strain

Answer 1

Hint: The shape of an object changes but the volume remains unchanged as a result of the action of the applied force. It can be explained by the ratio of a layer's displacement to its distance from the fixed layer. As a result, the stress that develops within the body is known as shearing stress.

Formula used:
Shearing strain = Δx / h = tan Ф


Complete answer:
Changing the motion of objects is the responsibility of forces. The shape of an object can change if more than one force is existent. When a force acts on an object, it can change shape by bending, stretching, or compressing - or by a combination of all three. To change the shape of a stationary object, nevertheless, more than one force must be acting. Deformation refers to a change in shape.
Assume ABCE is a square-shaped body (Figure). A tangential force 'F' is applied to side AB by keeping side CE fixed. Allow points A and B to be shifted to A′ and B′, respectively, due to the action of the applied force. The original shape of the cube ABCE has now been transformed into a rhombus A′B′CE. As a result, the shape of the object has changed. This is known as shearing strain.


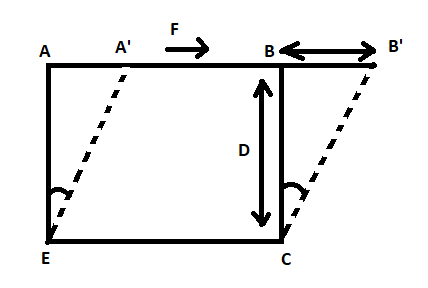
Shearing strain is defined as the ratio of the change in dimension (Δx) caused due to the force to the distance between the fixed layer and the point of action of the force (h).
Shearing strain = Δx / h = tan Ф
In reference to the above diagram,
The angular displacement measures the shearing strain. Allowing for a very small angular displacement of θ,
Shearing strain, = d/D (as we all know, = tan θ = d/D)
As a result, shearing strain = [Relative displacement / intervening distance]
The correct option is (B).



Note: A shearing strain is never associated with a volume change. That is, when subjected to shear strain, the body is distorted, but only in shape, not in size. That's why volume stress is not a reason for the change in shape whereas it changes size. While the longitudinal strain is when stress (external force per unit area) is applied to the body, the deforming force alone causes a shift in length, and the body surpasses its elastic limit.