
The output Y of the logic circuit given below is:-
A. \[1\]
B. \[0\]
C. \[X\]
D. \[\overline X \]
Answer
216k+ views
Hint: Here in this question, we need to determine the output of the logic circuit. The given circuit is a combination of the two gates, first is a NOT gate, and the second is the XOR gate, the output from the NOT gate will be one of the inputs for the XOR gate in the circuit, using the TRUTH TABLE we will find the result.
Complete step by step solution:
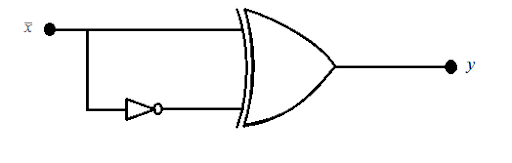
In the given circuit we can see the first logical gate is the NOT gate and the second logical gate is the XOR gate. The input \[\overline X \] to the logical circuit is first divided by the parallel circuit, one going direct to the XOR gate and another through the NOT gate.
When a binary input is given to a NOT gate then the signal is INVERTED so the signal \[\overline X \] will become \[X\].
Now, we will find the output Y of the XOR gate, when its inputs are \[\overline X \] and \[X\], to find the same we will draw a truth table-
Now from the above table we will write the equation for the high output signals, we have
\[y = X \oplus \overline X \\y = X\overline X + \overline X X\]
On further solving this, we have
\[y = XX + \overline X \overline X \]
Now, by using the inverse law \[A + \overline A = 1\], we can write-
\[y = X + \overline X \,\\ \therefore y = 1\]
Therefore, we get the output Y of the logic circuit as \[1\].
Hence, option A is correct.
Note: Always note that a XOR gate gives a true output when the number of logical inputs is odd, \[y = A\overline B + \overline A B\] and \[y = A\overline {BC} + \overline A B\overline C + \overline {AB} C + ABC\].
Complete step by step solution:
In the given circuit we can see the first logical gate is the NOT gate and the second logical gate is the XOR gate. The input \[\overline X \] to the logical circuit is first divided by the parallel circuit, one going direct to the XOR gate and another through the NOT gate.
When a binary input is given to a NOT gate then the signal is INVERTED so the signal \[\overline X \] will become \[X\].
Now, we will find the output Y of the XOR gate, when its inputs are \[\overline X \] and \[X\], to find the same we will draw a truth table-
| \[\overline X \] | \[X\] | Output \[y = \overline X \oplus X\] |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Now from the above table we will write the equation for the high output signals, we have
\[y = X \oplus \overline X \\y = X\overline X + \overline X X\]
On further solving this, we have
\[y = XX + \overline X \overline X \]
Now, by using the inverse law \[A + \overline A = 1\], we can write-
\[y = X + \overline X \,\\ \therefore y = 1\]
Therefore, we get the output Y of the logic circuit as \[1\].
Hence, option A is correct.
Note: Always note that a XOR gate gives a true output when the number of logical inputs is odd, \[y = A\overline B + \overline A B\] and \[y = A\overline {BC} + \overline A B\overline C + \overline {AB} C + ABC\].
Recently Updated Pages
Wheatstone Bridge Explained: Working, Formula & Uses

Young’s Double Slit Experiment Derivation Explained

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

JEE Main Correction Window 2026 Session 1 Dates Announced - Edit Form Details, Dates and Link

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Atomic Structure: Definition, Models, and Examples

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance




