
The number of real roots of the equation ${\log _e}x + ex = 0$
$
{\text{A}}{\text{. 0(zero)}} \\
{\text{B}}{\text{. 1}} \\
{\text{C}}{\text{. 2}} \\
{\text{D}}{\text{. 3}} \\
$
Answer
224.4k+ views
Hint: -You can solve this question by two method first simply solve and get value of x and check whether it is real or not and we can see there is only two terms so, put one term one side of equal to and another term on opposite side of equal to and draw graph of both to solve further.
Complete step-by-step solution -
From given
${\log _e}x + ex = 0$
You can write it as
${\log _e}x = - ex$
Now you have to draw the graph of $y = {\log _e}x$ and graph of y = -ex .
You should have knowledge of graphs of logarithmic function and also knowledge of graphs of straight line. Now you have to check the cutting points of both the graphs.
So, you can see in diagram graph cuts each other at only one point so there is only one real root of the equation.
Hence option B is the correct option.
Note: -Whenever you get this type of question the key concept of solving is you have to draw a graph of function and check the cutting points. Real roots means simply cutting points of the graphs. But you should have knowledge of drawing graphs. Drawing graphs and checking real roots are the best way of solving a number of real roots questions.
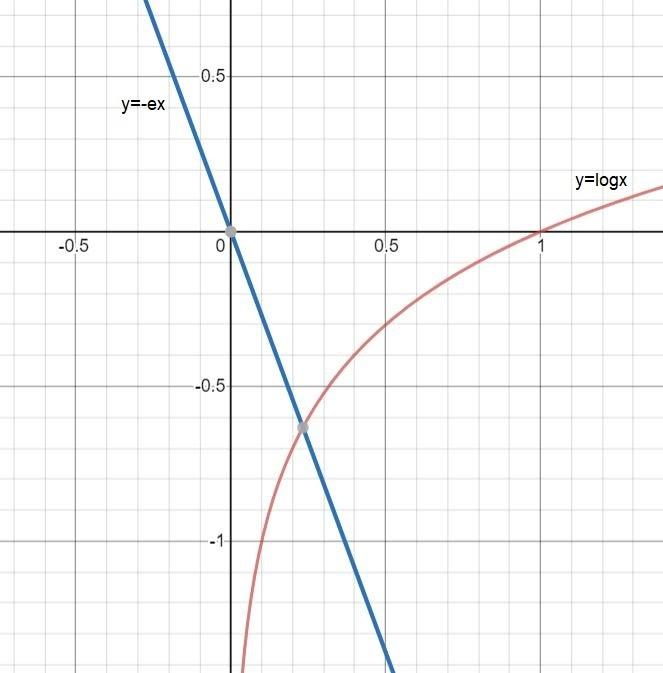
Complete step-by-step solution -
From given
${\log _e}x + ex = 0$
You can write it as
${\log _e}x = - ex$
Now you have to draw the graph of $y = {\log _e}x$ and graph of y = -ex .
You should have knowledge of graphs of logarithmic function and also knowledge of graphs of straight line. Now you have to check the cutting points of both the graphs.
So, you can see in diagram graph cuts each other at only one point so there is only one real root of the equation.
Hence option B is the correct option.
Note: -Whenever you get this type of question the key concept of solving is you have to draw a graph of function and check the cutting points. Real roots means simply cutting points of the graphs. But you should have knowledge of drawing graphs. Drawing graphs and checking real roots are the best way of solving a number of real roots questions.

Recently Updated Pages
JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

Isoelectronic Definition in Chemistry: Meaning, Examples & Trends

Ionisation Energy and Ionisation Potential Explained

Iodoform Reactions - Important Concepts and Tips for JEE

Introduction to Dimensions: Understanding the Basics

Instantaneous Velocity Explained: Formula, Examples & Graphs

Trending doubts
JEE Main 2026: City Intimation Slip Releasing Today, Application Form Closed, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Hybridisation in Chemistry – Concept, Types & Applications

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

Understanding Electromagnetic Waves and Their Importance

Understanding Atomic Structure for Beginners




