Question

What should be the mass m so that the block moves upward with constant velocity?

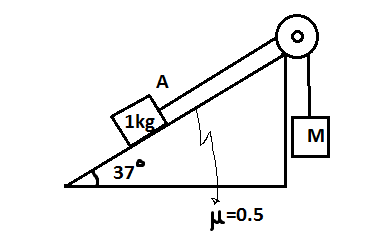
A.4kg
B.3kg
C.2kg
D.1kg

Answer 1

Hint: A body is said to move with constant velocity if and only if the net acceleration is zero. So , the mass of the block hangin should be such that all the forces are balanced.

Complete solution
For a body to move with constant velocity it must have zero net acceleration. Net acceleration is zero means the net force acting on the body is zero. This means that all forces should be balanced. Thus mass of the block hanging should be such that all force acting on the sliding block should cancel each other. This problem is based on force balancing so let us draw the FBD (free body diagram) of the bodies. The FBD of the two blocks is given below;



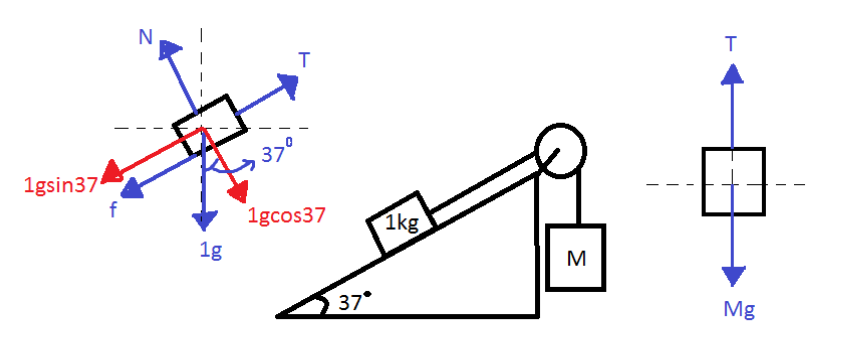
The FBD shows us how the forces are acting on the bodies.
Now let us balance the forces acting on the bodies;
Case 1: The block with mass 1kg-
Balancing the forces along the body:
$1g\sin {37^ \circ } + f = T$ (equation: 1)
Balancing forces normal to the body:
$N = 1g\cos {37^ \circ }$
Thus, $N = 1 \times 10 \times \dfrac{4}{5} = 8N$ (equation: 2)
Now by definition of friction we get;
$f = \mu N$
From equation: 2 we substitute the value of N
${f_{\max }} = 0.5 \times 8 = 4N$ (equation: 3)
Here, friction is considered to be maximum because if maximum friction is balanced the and only then there will be no net acceleration. If there is no acceleration for maximum friction there won’t be any acceleration for any other value of friction. Thus we will get the minimum mass required to satisfy the case.
Case 2: Block of mass M-
Balancing forces in the vertical direction, we get;
$T = Mg$ (equation: 4)
Now, from equation 4, equation 3 and equation 1 we get;
$1g\sin {37^ \circ } + 4 = Mg$
Solving this equation further will give us the minimum value of mass required for moving the block with constant velocity;
$1 \times 10 \times \dfrac{3}{5} + 4 = 10M$
$6 + 4 = 10M$
$10M = 10$
Hence, $M = 1$

Therefore option D is correct.

Note: (1) If you do not consider the maximum friction here then your answer will be valid for that particular value of friction and will not be a general answer for the problem.
Also the product of coefficient of friction and normal force gives us the maximum friction of the surface.
(2) If the string is an ideal non-expanding string then tension in all parts will be uniform.